(本小题满分12分)
已知数列 ,且
,且 是函数
是函数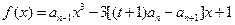 ,(
,( )的一个极值点.数列
)的一个极值点.数列 中
中 (
(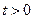 且
且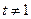 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)记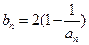 ,当
,当 时,数列
时,数列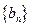 的前
的前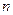 项
项 和为
和为 ,求使
,求使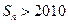 的
的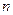 的最小值;
的最小值;
(3)若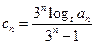 ,证明:
,证明: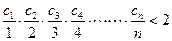 (
(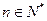 )。
)。
甲、乙两支足球队,苦战120分钟,比分为1 :1,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员点球命中率均为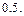
⑴两队球员一个间隔一个出场射球,有多少种不同的出场顺序?
⑵甲、乙两队各射完5个点球后,再次出现平局的概率是多少?
某同学上楼梯的习惯每步走1阶或2阶,现有一个11阶的楼梯 ,该同学从第1阶到第11阶用7步走完。
(1)求该同学恰好有连着三步都走2阶的概率;
(2)记该同学连走2阶的最多步数为ζ,求随机事件ζ的分布列及其期望。
 某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
某售货员负责在甲、乙、丙三个柜面上售货.如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8,0.7.假定各个柜面是否需要照顾相互之间没有影响,求在这个小时内:
(1)只有丙柜面需要售货员照顾的概率;
(2)三个柜面最多有一个需要售货员照顾的概率;
(3)三个柜面至少有一个需要售货员照顾的概率.
从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为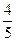 ,每个乙品牌元件能通过测试的概率均为
,每个乙品牌元件能通过测试的概率均为 .试求:
.试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率;
(II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.
袋里装有30个球,每个球上都记有1到30的一个号码, 设号码为 的球的重量为
的球的重量为 (克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.
(克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.
(Ⅰ)如果任意取出1球, 求其号码是3的倍数的概率.
(Ⅱ)如果任意取出1球, 求重量不大于号其码的概率;
(Ⅲ)如果同时任意取出2球, 试求它们重量相同的概率.