某中学一位高三班主任对本班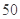 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| |
积极参加班级工作 |
不太主动参加班级工作 |
合计 |
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
已知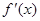 是
是 的导函数,
的导函数,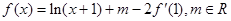 ,且函数
,且函数 的图象过点
的图象过点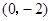 .
.
(1)求函数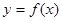 的表达式;
的表达式;
(2)求函数 的单调区间和极值.
的单调区间和极值.
如图,在四棱锥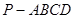 中,底面
中,底面 为矩形,
为矩形,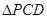 为等边三角形,
为等边三角形,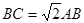 ,点
,点 为
为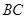 中点,平面
中点,平面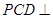 平面
平面 .
.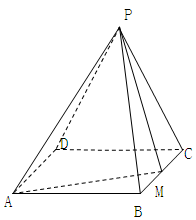
(1)求异面直线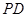 和
和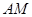 所成角的余弦值;
所成角的余弦值;
(2)求二面角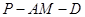 的大小.
的大小.
已知椭圆C: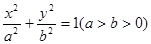 的左、右焦点分别为
的左、右焦点分别为 ,离心率
,离心率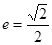 ,连接椭圆的四个顶点所得四边形的面积为
,连接椭圆的四个顶点所得四边形的面积为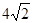 .
.
(1)求椭圆C的标准方程;
(2)设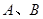 是直线
是直线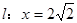 上的不同两点,若
上的不同两点,若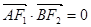 ,求
,求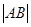 的最小值.
的最小值.
已知命题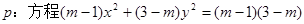 表示的曲线是双曲线;命题
表示的曲线是双曲线;命题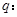 函数
函数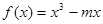 在区间
在区间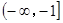 上为增函数,若“
上为增函数,若“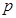
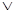
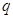 ”为真命题,“
”为真命题,“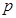

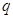 ”为假命题,求实数
”为假命题,求实数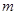 的取值范围.
的取值范围.
如图,在底面为平行四边形的四棱锥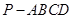 中,
中,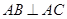 ,
, 平面
平面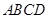 ,且
,且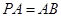 ,点
,点 是
是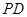 的中点.
的中点.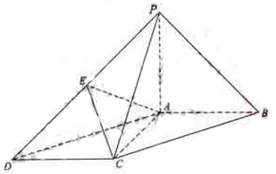
(1)求证: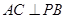 ;
;
(2)求证: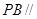 平面
平面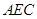 ;
;
(3)求二面角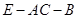 的大小.
的大小.