一个正方体物体沿斜坡向上滑动,其截面如图所示,正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米,则:
(1)AC的长是 米;
(2)当正方体DEFH运动到什么位置,即当AE= 米时,有DC2=AE2+BC2.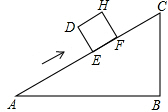
如图,已知抛物线 与 轴交于点 和点 ,与 轴交于点 ,连接 交抛物线的对称轴于点 , 是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点 和点 的坐标;
(3)若点 在第一象限内的抛物线上,且 ,求 点坐标.
注:二次函数 的顶点坐标为 ,

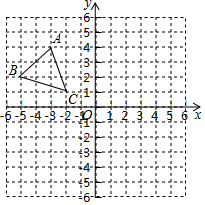
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度, 的三个顶点的坐标分别为 , , .
(1)画出 关于 轴的对称图形△ ;
(2)画出将 绕原点 逆时针方向旋转 得到的△ ;
(3)求(2)中线段 扫过的图形面积.
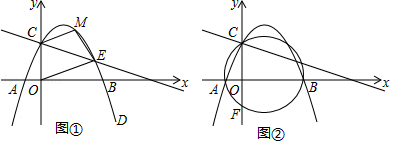
在平面直角坐标系中,二次函数 的图象经过点 和点 .点 是直线 与二次函数图象在第一象限内的交点.
(1)求二次函数的解析式及点 的坐标.
(2)如图①,若点 是二次函数图象上的点,且在直线 的上方,连接 , , .求四边形 面积的最大值及此时点 的坐标.
(3)如图②,经过 、 、 三点的圆交 轴于点 ,求点 的坐标.
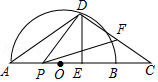
如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .
(1)求 的长.
(2)点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.
在水果销售旺季,某水果店购进一优质水果,进价为20元 千克,售价不低于20元 千克,且不超过32元 千克,根据销售情况,发现该水果一天的销售量 (千克)与该天的售价 (元 千克)满足如下表所示的一次函数关系.
|
销售量 (千克) |
|
34.8 |
32 |
29.6 |
28 |
|
|
售价 (元 千克) |
|
22.6 |
24 |
25.2 |
26 |
|
(1)某天这种水果的售价为23.5元 千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?