如图1，某超市从一楼到二楼的电梯AB的长为16.50米，坡角∠BAC为32°．
（1）求一楼与二楼之间的高度BC（精确到0.01米）；
（2）电梯每级的水平级宽均是0.25米，如图2．小明跨上电梯时，该电梯以每秒上升2级的高度运行，10秒后他上升了多少米（精确到0.01米）？备用数据：sin32°=0.5299，cos32°=0.8480，tan32°=0.6249．
（1）画出数轴，并用数轴上的点表示下列各数：
-5，2.5，3，-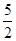
，0，-3，3
．
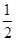（2）用“＜”号把各数从小到大连起来：
（本题7分）如图所示，用三种大小不同的六个正方形和一个缺角的正方形拼成长方形ABCD,
其中，GH="2cm," GK="2cm," 设BF=xcm,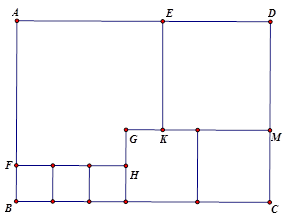
（1）用含x的代数式表示CM=cm, DM=cm．
（2）求长方形ABCD的面积．
（本题7分）某自行车厂一周计划生产2100辆电动车，平均每天生产电动车300辆，由于各种原因，实际每天生产量与计划每天生产量相比有出入。下表是某周的生产情况（超产记为正、减产记为负，单位：辆）：
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
日 |
| 减增 |
+8 |
-2 |
-6 |
+11 |
-12 |
+6 |
+7 |
（1）根据记录的数据可知，该厂星期一生产电动车辆
（2）产量最多的一天比产量最少的一天多生产电动车辆
（3）该厂实行记件工资制，每生产一辆车可得60元，若超额完成任务，则超额部分每辆车另奖10元，每少生产一辆扣10元，那么该厂工人这一周的工资总额是多少元？
（本题满分10分，每小题5分）先化简，后求值：
（1）5（3x2y－xy2）－3（－xy2＋4x2y），其中x＝1，y＝－
．
（2）
, 其中
=2014．
（本题4分）把下列各数-12，
，
，+（+2），在数轴上表示出来，并用“＞”把他们连接起来．