甲、乙玩转盘游戏时，把质地相同的两个转盘A、B平均分成2份和3份，并在每一份内标有数 字如图．游戏规则：甲、乙两人分别同时转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数 时甲获胜；数字之和为奇数时乙获胜．若指针落在分界线上，则需要重新转动转盘．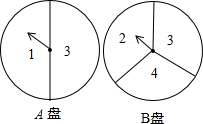
（1）用画树状图或列表的方法，求甲获胜的概率；
（2）这个游戏对甲、乙双方公平吗？请判断并说明理由．
如图，已知AB=AC，AD=AE，点D、E在线段BC上。问：BE=CD成立吗?并说明理由。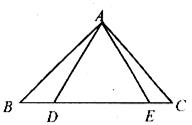
解方程组
（1）
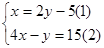（2）
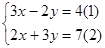
△ABC在平面直角坐标系中的位置如图所示。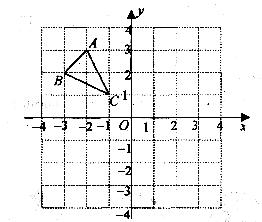
（1）作出△ABC关于x轴对称的△A1B1C1；
（2）将△ABC向右平移4个单位长度，画出平移后的△A2B2C2。
如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB=45°
（1）求证：AG=FG;
（2）延长FC、AE交于点M，连接DF、BM，若C为FM中点，BM=10，求FD的长.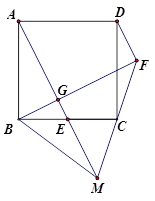
如图，平面直角坐标系中O为坐标原点，直线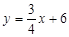
与x轴、y轴分别交于A、B两点，C为OA中点；
（1）求直线BC解析式；
（2）动点P从O出发以每秒2个单位长度的速度沿线段OA向终点A运动，同时动点Q从C出发沿线段CB以每秒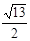
个单位长度的速度向终点B运动，过点Q作QM∥AB交x轴于点M，若线段PM的长为y，点P运动时间为t( )，求y于t的函数关系式；
（3）在（2）的条件下，以PC为直径作⊙N，求t为何值时直线QM与⊙N相切.