①xy•(x﹣y+1)
②﹣3a(4a2﹣ a+
a+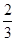 b)
b)
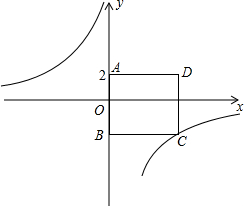
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数
的图象经过点C,一次函数
的图象经过点
,一次函数
的图象经过点
, 
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
如图,已知直线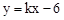 与抛物线
与抛物线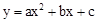 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。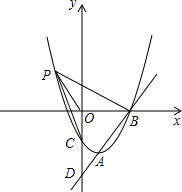
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立。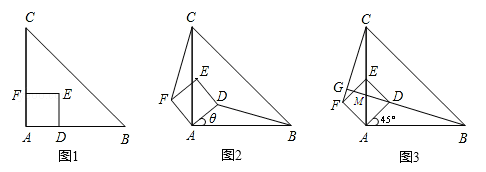
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由。
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G。
求证:BD⊥CF。
(3)在(2)小题的条件下, AC与BG的交点为M, 当AB=4,AD=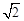 时,求线段CM的长。
时,求线段CM的长。
如图,反比例函数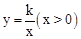 的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=
的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=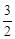 。
。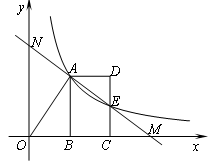
(1)求k的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数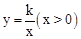 的图象恰好经过DC的中点E,求直线AE的函数表达式;
的图象恰好经过DC的中点E,求直线AE的函数表达式;
(3)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.
“五·一”假期,某公司组织部分员工分别到A、B、C、D四地旅游,公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图,根据统计图回答下列问题: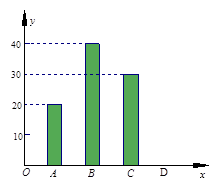
(1)若去D地的车票占全部车票的10%,请求出D地车票的数量,并补全统计图;
(2)若公司采用随机抽取的方式分发车票,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小胡抽到去A地的概率是多少?
(3)若有一张车票,小王、小李都想要,决定采取抛掷一枚各面分别标有1,2,3,4的正四面体骰子的方法来确定,具体规则是:“每人各抛掷一次,若小王掷得着地一面的数字比小李掷得着地一面的数字小,车票给小王,否则给小李”.试用“列表法或画树状图”的方法分析,这个规则对双方是否公平?