“五·一”假期，某公司组织部分员工分别到A、B、C、D四地旅游，公司按定额购买了前往各地的车票.下图是未制作完的车票种类和数量的条形统计图，根据统计图回答下列问题：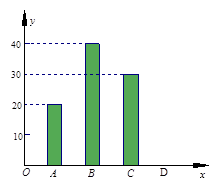
（1）若去D地的车票占全部车票的10%，请求出D地车票的数量，并补全统计图；
（2）若公司采用随机抽取的方式分发车票，每人抽取一张（所有车票的形状、大小、质地完全相同且充分洗匀），那么员工小胡抽到去A地的概率是多少？
（3）若有一张车票，小王、小李都想要，决定采取抛掷一枚各面分别标有1，2，3，4的正四面体骰子的方法来确定，具体规则是：“每人各抛掷一次，若小王掷得着地一面的数字比小李掷得着地一面的数字小，车票给小王，否则给小李”.试用“列表法或画树状图”的方法分析，这个规则对双方是否公平？
先化简，再求值：
，其中
是不等式组
的整数解
如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．
（1）求这条抛物线的解析式；
（2）设D（m，n），矩形ABCD的周长为l，写出l与m的关系式，并求出l的最大值；
（3）点E在抛物线的对称轴上，在抛物线上是否还存在点F，使得以E、F、O、M为顶点的四边形是平行四边形？如果存在，写出F点的坐标．
如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A．与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．
（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC，AD，BC之间的数量关系，并说明理由．
如图，将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，且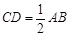
，已知AC=8cm，BC=6cm，求线段DD′的长．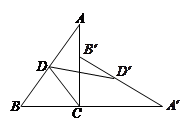
一个盒子里有完全相同的三个小球，球上分别标上数字﹣1、1、2．随机摸出一个小球（不放回）其数字记为p，再随机摸出另一个小球其数字记为q，求满足关于x的方程x2+px+q=0有实数根的概率．