（本小题满分10分）选修4—4：坐标系与参数方程
以直角坐标系的原点
为极点，
轴的正半轴为极轴，已知点P的直角坐标为（1，－5），点M的极坐标为（4，
），若直线
过点P，且倾斜角为
，圆C以M为圆心，4为半径。
（1）求直线的参数方程和圆C的极坐标方程。
（2）试判定直线与圆C的位置关系。
如图，正在海上A处执行任务的渔政船甲和在B处执行任务的渔政船乙，同时收到同一片海域上一艘渔船丙的求救信号，此时渔船丙在渔政船甲的南偏东40°方向距渔政船甲70km的C处，渔政船乙在渔政船甲的南偏西20°方向的B处，两艘渔政船协调后立即让渔政船甲向渔船丙所在的位置C处沿直线AC航行前去救援，渔政船乙仍留在B处执行任务，渔政船甲航行30km到达D处时，收到新的指令另有重要任务必须执行，于是立即通知在B处执行任务的渔政船乙前去救援渔船丙（渔政船乙沿直线BC航行前去救援渔船丙），此时B、D两处相距42km，问渔政船乙要航行多少距离才能到达渔船丙所在的位置C处实施营救．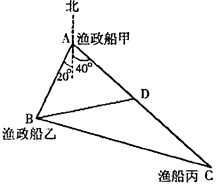
在数列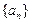
中，
，
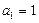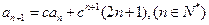其中实数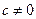
．
(1)用归纳法求数列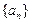的通项公式；
(2) 用数学归纳法证明你的结论．
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目，对甲、乙两名运动员进行培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次，得出茎叶图如图所示．
甲 |
乙 |
||||
| 9 |
8 |
7 |
5 |
||
| 4 |
1 |
8 |
0 |
3 |
5 |
| 5 |
3 |
9 |
2 |
5 |
(1)从平均成绩
及发挥稳定性的角度考虑，你认为选派哪名运动员合适？
(2)若将频率视为概率，对甲运动员在今后的3次比赛成绩进行预测，记这3次成绩中高于80分的次数为ξ，求ξ的分布列及数学期望E(ξ)
已知函数f(x)=In(1+x)-
+
(
≥0)。
(1)当=2时，求曲线y=f(x)在点(1，f(1))处的切线方程；
(2)求函数f(x)的单调区间。
(1)
个人坐在一排
个座位上,问①空位不相邻的坐法有多少种?②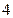 
个空位只有
个相邻的坐法有多少种
?
(2) 
的展开式奇数项的二项式系数之和为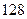
，则求展开式中二项式系数最大项。