(本小题满分16分)已知奇函数 的定义域为
的定义域为 ,当
,当 时,
时, .
.
(1)求函数 在
在 上的值域;
上的值域;
(2)若 ,y=
,y= 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
(本小题共13分)已知函数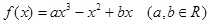 ,
,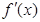 为其导函数,且
为其导函数,且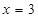 时
时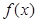 有极小值
有极小值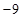 .
.
(Ⅰ)求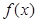 的单调递减区间;
的单调递减区间;
(Ⅱ)若不等式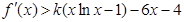 (为正整数)对任意正实数恒成立,求的最大值.(解答过程可参考使用以下数据:
(为正整数)对任意正实数恒成立,求的最大值.(解答过程可参考使用以下数据: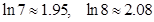 )
)
(本小题共14分)已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,焦距为2,离心率为
轴上,焦距为2,离心率为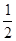 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设直线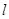 经过点
经过点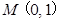 ,且与椭圆
,且与椭圆 交于
交于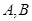 两点,若
两点,若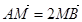 ,求直线
,求直线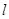 的方程.
的方程.
(本小题共13分)某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
| 分组 |
频数 |
频率 |
|
| 第1组 |
[60,70) |
M |
0.26 |
| 第2组 |
[70,80) |
15 |
p |
| 第3组 |
[80,90) |
20 |
0.40 |
| 第4组 |
[90,100] |
N |
q |
| 合计 |
50 |
1 |
(Ⅰ)写出M 、N 、p、q(直接写出结果即可),并作出频率分布直方图;
(Ⅱ)若成绩在90分以上的学生获得一等奖,试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)现从所有一等奖的学生中随机选择2名学生接受采访,已知一等奖获得者中只有2名女生,求恰有1名女生接受采访的概率.
(本小题共14分)如图所示,在正方体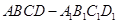 中,
中,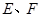 分别是棱
分别是棱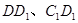 的中点.
的中点.
(Ⅰ)证明:平面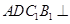 平面
平面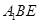 ;
;
(Ⅱ)证明: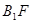 //平面
//平面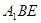 ;
;
(Ⅲ)若正方体棱长为1,求四面体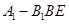 的体积.
的体积.
(本小题共13分)已知函数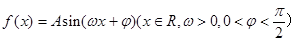 的部分图象如图所示.
的部分图象如图所示.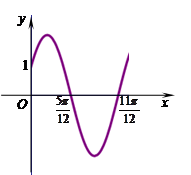
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求函数 在区间
在区间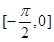 上的最大值与最小值.
上的最大值与最小值.