(本小题满分12分)已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)试确定函数 的解析式;
的解析式;
(2)若 ,求
,求 的值.
的值.
已知等差数列{an}的首项a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项,第三项,第四项.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n,均有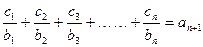 ,
,
求c1+c2+c3+……+c2006值.
某城市2001年底人口为500万,人均住房面积为6 m2,如果该城市每年人口平均增长率为1%,则从2002年起,每年平均需新增住房面积为多少万m2,才能使2020年底该城市人均住房面积至少为24m2?(可参考的数据1.0118=1.20,1.0119=1.21,1.0120=1.22).
已知:等差数列{ }中,
}中,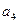 =14,前10项和
=14,前10项和 .
.
(1)求 ;
;
(2)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和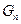 .
.
在等比数列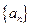 中,
中,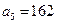 ,公比
,公比 ,前
,前 项和
项和 ,求首项
,求首项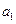 和项数
和项数
)已知x、y满足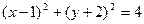 ,求
,求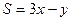 的最值
的最值