如图，在直角梯形ABCD中，AD∥BC，∠C＝90°，BC＝16，DC＝12，AD＝21。动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q从点C出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C同时出发，当点Q运动到点B时，点P随之停止运动。设运动的时间为t（秒）。
（1）设△BPQ的面积为S，求S与t之间的函数关系式；
（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？
（3）是否存在时刻t，使得PQ⊥BD？若存在，求出t的值；若不存在，请说明理由。
如图，将△ＡＢＣ绕点Ｏ顺时针旋转180°后得到△
.请你画出旋转后的△；
请你画出下面“蒙古包”的左视图．
如图，已知∠1=∠2,AO=BO.求证：AC=BC.
先化简，再选择一个你喜欢的数代入求值．
计算：
如图1，将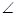
EAF绕着四边形ABCD的顶点A顺时针旋转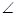，EAF的两边分别与DC的延长线交于点F，与CB的延长线交于点E，连接EF。
若四边形ABCD为正方形，当
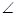EAF=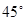
时，EF与DF、BE之间有怎样的数量关系？（只需直接写出结论）如图2，如果四边形ABCD中，AB=AD，
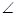ABC与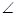ADC互补，当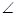EAF=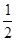 
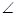BAD时，EF与DF、BE之间有怎样的数量关系？请写出它们之间的关系式并给予证明。在（2）中，若BC=4，DC=7，CF=2，求
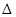CEF的周长（直接写出结果即可）。