如图①，正方形 ABCD中，点A、B的坐标分别为（0，10），（8，4），
点C在第一象限．动点P在正方形 ABCD的边上，从点A出发沿A→B→C→D匀速运动，
同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，
设运动的时间为t秒．
（1）当P点在边AB上运动时，点Q的横坐标
（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；
（2）求正方形边长及顶点C的坐标；
（3）在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；
（4）如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，写出所有符合条件的t的值；若不能，请说明理由．
（本题8分）计算：（1）
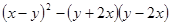
（2）
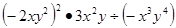
已知△PQR在直角坐标系中的位置如图所示：
(1) 求出△PQR的面积；
(2) 画出△P′Q′R′，使△P′Q′R′与△PQR关于y轴对称，写出点P′、Q′、R′的坐标；
(3)连接PP′，QQ′，判断四边形QQ′P′P的形状，求出四边形QQ′P′P的面积。
因式分解 ： （1）
（2）
如图，在网格中有两个全等的图形(阴影部分)，用这两个图形拼成轴对称图形，试分别在图(1)、(2)中画出两种不同的拼法． 
.(12分)如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10。动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒。（1）写出数轴上点B表示的数 ，点P表示的数 （用含t的代数式表示）；
（2）动点R从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、R同时出发，问点P运动多少秒时追上点R？
（3）若M为AP的中点，N为PB的中点。点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；
