已知x∈[ , 2], 求函数y=
, 2], 求函数y= 的最小值.
的最小值.
已知某精密仪器生产总成本C(单位:万元)与月产量x(单位:台)的函数关系为 ,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为
,月最高产量为150台,出厂单价p(单位:万元)与月产量x的函数关系为 .
.
(1)求月利润L与产量x的函数关系式 ;
;
(2)求月产量x为何值时,月利润 最大?
最大?
已知双曲线C的方程为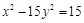 .
.
(1)求其渐近线方程;
(2)求与双曲线C焦点相同,且过点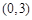 的椭圆的标准方程.
的椭圆的标准方程.
已知数列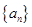 的前n项和
的前n项和 ;
;
(1)求数列的通项公式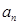 ;
;
(2)设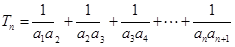 ,求
,求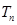
已知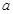 、
、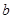 、
、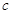 分别是
分别是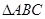 的三个内角
的三个内角 、
、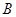 、
、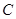 所对的边
所对的边
(1)若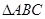 面积
面积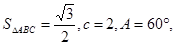 求
求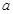 、
、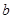 的值;
的值;
(2)若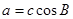 ,且
,且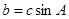 ,试判断
,试判断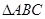 的形状.
的形状.
一条双曲线 的左、右顶点分别为
的左、右顶点分别为 ,点
,点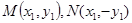 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。
(1)求直线 与
与 交点的轨迹
交点的轨迹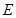 的方程式;
的方程式;
(2)设直线 与曲线
与曲线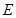 相交于不同的两点
相交于不同的两点 ,已知点
,已知点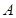 的
的 坐标为
坐标为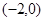 ,若点
,若点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 .求
.求 的值.
的值.