设不等式2x-1>m(x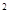 -1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
-1)对满足|m|≤2的一切实数m的取值都成立。求x的取值范围。
在极坐标系中,过曲线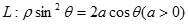 外的一点
外的一点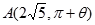 (其中
(其中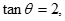
 为锐角)作平行于
为锐角)作平行于 的直线与曲线分别交于
的直线与曲线分别交于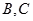 .
.
(1)写出曲线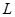 和直线的普通方程(以极点为原点,极轴为
和直线的普通方程(以极点为原点,极轴为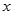 轴的正半轴建系);
轴的正半轴建系);
(2)若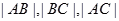 成等比数列,求
成等比数列,求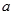 的值.
的值.
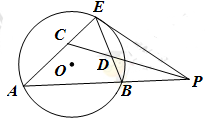
如图,已知 切⊙
切⊙ 于点
于点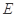 ,割线
,割线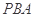 交⊙
交⊙ 于
于 两点,∠
两点,∠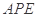 的平分线和
的平分线和 分别交于点
分别交于点 .
.
求证:(1) ;(2)
;(2)
已知函数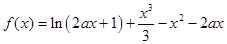 (
(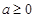 ).
).
(1)若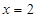 为
为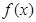 的极值点,求实数
的极值点,求实数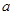 的值;
的值;
(2)若 在
在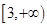 上不是单调函数,求实数
上不是单调函数,求实数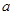 的取值范围;
的取值范围;
(3)当 时,方程
时,方程 有实根,求实数
有实根,求实数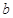 的最大值.
的最大值.
已知抛物线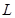 :
: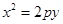 和点
和点 ,若抛物线
,若抛物线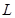 上存在不同两点
上存在不同两点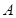 、
、 满足
满足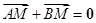 .
.
(1)求实数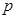 的取值范围;
的取值范围;
(2)当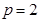 时,抛物线
时,抛物线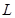 上是否存在异于
上是否存在异于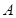 、
、 的点
的点 ,使得经过
,使得经过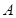 、
、 、
、 三点的圆和抛物线
三点的圆和抛物线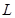 在点
在点 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
如图,四棱锥 中,
中, 平面
平面 ,
, 与底面所成的角为
与底面所成的角为 ,底面
,底面 为直角梯形,
为直角梯形, ,
,
(1)求证:平面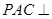 平面
平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使
,使 与平面
与平面 所成的角为
所成的角为 ?若存在,确定点
?若存在,确定点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.