(本小题满分10分,几何证明选讲)
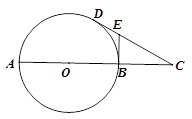
如图,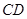 是圆
是圆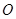 的切线,切点为
的切线,切点为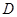 ,
,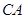 是过圆心的割线且交圆
是过圆心的割线且交圆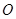 于
于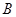 点,过
点,过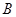 作
作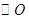 的切线交
的切线交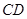 于点
于点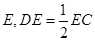 .
.
求证:(1)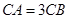 ;(2)
;(2)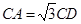 .
.
已知函数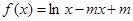 .
.
(Ⅰ)求函数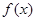 的单调区间;
的单调区间;
(Ⅱ)若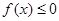 在
在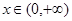 上恒成立,求实数
上恒成立,求实数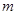 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,对任意的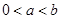 ,求证:
,求证: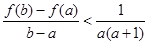 .
.
已知离心率为 的椭圆
的椭圆 的右焦点
的右焦点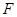 是圆
是圆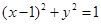 的圆心,过椭圆上的动点
的圆心,过椭圆上的动点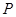 作圆的两条切线分别交
作圆的两条切线分别交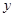 轴于
轴于 (与
(与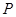 点不重合)两点.
点不重合)两点.
(Ⅰ)求椭圆方程;
(Ⅱ)求线段 长的最大值,并求此时点
长的最大值,并求此时点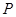 的坐标.
的坐标.
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,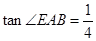 .
.
(Ⅰ)证明:平面ADE⊥平面ACD;
(Ⅱ)当三棱锥C-ADE体积最大时,求二面角D-AE-B的余弦值.
某超市从2014年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个,并按[0,10],(10,20],(20,30],(30,40],(40,50]分组,得到频率分布直方图如下:
假设甲、乙两种酸奶独立销售且日销售量相互独立.
(Ⅰ)写出频率分布直方图(甲)中的a的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为 ,
, ,试比较
,试比较 与
与 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅱ)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(Ⅲ)记X表示在未来3天内甲种酸奶的日销售量不高于20箱的天数,以日销售量落入各组的频率作为概率,求X的数学期望.
在 中,角
中,角 的对边分别为
的对边分别为 ,向量
,向量 ,向量
,向量 ,且
,且 :
:
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)设BC中点为D,且 :求a+2c的最大值及此时
:求a+2c的最大值及此时 的面积.
的面积.