如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=EB,AB=4,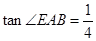 .
.
(Ⅰ)证明:平面ADE⊥平面ACD;
(Ⅱ)当三棱锥C-ADE体积最大时,求二面角D-AE-B的余弦值.
已知数列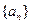 中,
中,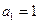 ,且
,且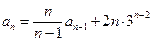
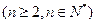
(Ⅰ) 求数列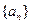 的通项公式;
的通项公式;
(Ⅱ) 令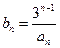
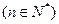 ,数列
,数列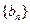 的前
的前 项和为
项和为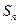 ,试比较
,试比较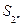 与
与 的大小;
的大小;
(Ⅲ) 令
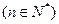 ,数列
,数列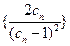 的前
的前 项和为
项和为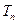 .求证:对任意
.求证:对任意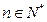 ,
,
都有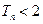 。
。
(文科做)已知函数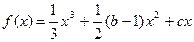 (b、c为常数).
(b、c为常数).
(1) 若 在
在
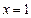 和
和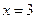 处取得极值,试求
处取得极值,试求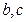 的值;
的值;
(2) 若 在
在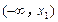 、
、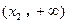 上单调递增,且在
上单调递增,且在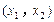 上单调递减,又满足
上单调递减,又满足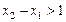 ,求证:
,求证: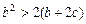 。
。
(理科做)已知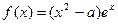
(I)若a=3,求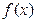 的单调区间和极值;
的单调区间和极值;
(II)已知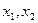 是
是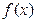 的两个不同
的两个不同 的极值点,且
的极值点,且 ,若
,若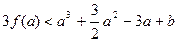 恒成立,求实数
恒成立,求实数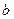 的取值范围。
的取值范围。
在△ABC中,角A,B,C所对边分别为a,b,c,且 .
.
(Ⅰ)求角A;
(Ⅱ)若m ,n
,n ,试求|m
,试求|m n|的最小值。
n|的最小值。
公差不为0的等差数列 中,
中, 且
且 成等比数列.
成等比数列.
(I)求数列 的通项公式和它的前20项和
的通项公式和它的前20项和 .
.
(II) 求数列 前n项的和
前n项的和 .
.