(文科做)已知函数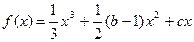 (b、c为常数).
(b、c为常数).
(1) 若 在
在
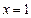 和
和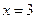 处取得极值,试求
处取得极值,试求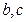 的值;
的值;
(2) 若 在
在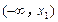 、
、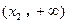 上单调递增,且在
上单调递增,且在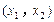 上单调递减,又满足
上单调递减,又满足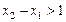 ,求证:
,求证: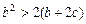 。
。
如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.试探究点M的位置,使F—AE—M为直二面角
.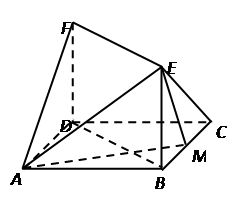
已知双曲线C的中心在原点,抛物线 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线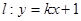 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若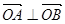 ,求实数k值.
,求实数k值.
图形P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=AB,Q是PC中点.AC,BD交于O点.
(1)二面角Q-BD-C的大小:
(2求二面角B-QD-C的大小.
设函数
(1)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(2)设 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的长.
的三个内角的大小和AC边的长.
已知二次函数
(1)若 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的 ,且
,且 <
< ,
, (
( >0),试证明:
>0),试证明: >
> 成立。
成立。
(3)是否存在 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意 ,
, ,且
,且 ②对任意的
②对任意的 ,都有
,都有 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。