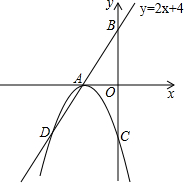（1）请找出下图中每个正多边形对称轴的条件，并填入下表．
| 正多边形的边数 |
3 |
4 |
5 |
6 |
8 |
… |
| 对称轴的条数 |
3 |
4 |
5 |
|
|
… |
（2）请写出正多边形的对称轴的条数y随正多边形的边数n（n≥3）变化的关系式y="n" ．
已知：如图，在
中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．
（1）求证：△DOE≌△BOF．
（2）当∠DOE等于多少度时，四边形BFDE为菱形?请说明理由．
某校为了了解学生孝敬父母的情况（选项：A为父母洗一次脚；B帮父母做一次家务；C给父母买一件礼物；D其它），在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：
根据以上信息解答下列问题：
（1）这次被调查的学生有多少人?
（2）求表中m，n，p的值，并补全条形统计图．
（3）该校有1600名学生，估计该校全体学生中选择B选项的有多少人?
解方程：
．
（1）计算；
；
（2）化简：
．
如图，直线AB的解析式为y=2x+4，交x轴于点A，交y轴于点B，以A为顶点的抛物线交直线AB于点D，交y轴负半轴于点C（0，﹣4）．
（1）求抛物线的解析式；
（2）将抛物线顶点沿着直线AB平移，此时顶点记为E，与y轴的交点记为F，
①求当△BEF与△BAO相似时，E点坐标；
②记平移后抛物线与AB另一个交点为G，则S△EFG与S△ACD是否存在8倍的关系？若有请直接写出F点的坐标．