如图,等腰Rt△ABD中,AB=AD,点M 为边AD上一动点,点E在DA的延长线上,且AM=AE,以BE为直角边,向外作等腰Rt△BEG,MG交AB于N,连NE、DN.
(1)求证:∠BEN=∠BGN.
(2)求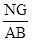 的值.
的值.
(3)当M在AD上运动时,探究四边形BDNG的形状,并证明之.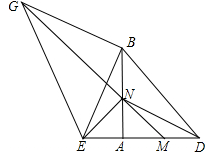
本题满分7分.
如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB,BC各为多少米?
(本题满分7分.为方便答题,可在答卷上画出你认为必要的图形)
如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.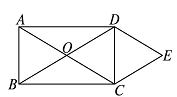
求证:四边形OCED是菱形.
解方程:x(x-2)+x-2=0.
(本题10分)如图①,点O为直线AB上一点,过O点作射线OC,使∠BOC=120o,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板绕点O按逆时针方向旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:直线ON是否平分∠AOC?请说明理由.
(2)将图①中的三角板绕点O按每秒6o的速度逆时针方向旋转一周,在旋转的过程中,直线ON恰好平分∠AOC,求旋转时间t的值.
(3)将图①中的三角板绕点O按顺时针方向旋转至图③的位置,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,请说明理由.
(本题10分)如图,点C是线段AB的中点.
(1)若点D在线段CB上,且DB=3.5cm,AD=6.5cm,求线段CD的长度;
(2)若将(1)中的点“D在线段CB上”改为“点D在直线CB上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度;
(3)若线段AB="12" cm,点C在AB上,点D、E分别是AC和BC的中点.
①当点C恰是AB中点时,则DE=cm.
②当AC=4cm,时,求DE的长;
③当点C在线段AB上运动时(点C与A、B重合除外),求DE的长.