如图,△ABC中,中线BD,CE相交于O.F、G分别为BO,CO的中点.
(1)求证:四边形EFGD是平行四边形;
(2)若△ABC的面积为12,求四边形EFGD的面积.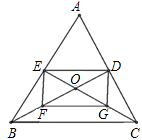
已知关于x的一元二次方程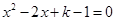 .
.
(1)若此方程有两个不相等的实数根,求实数k的取值范围;
(2)已知x=3是此方程的一个根,求方程的另一个根及k的值;
解方程:(1)x(x+2)=5x+10
(2)3x2-6x+1=0
如图,直径为10的⊙O经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+48=0的两根。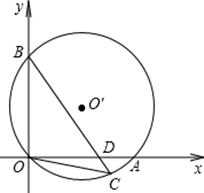
(1)求线段OA、OB的长;
(2)已知点C在劣弧OA上,连结BC交OA于D,当OC2=CD·CB时,求C点的坐标;
(3)在⊙O上是否存在点P,使S△POD=S△ABD.若存在,求出点P的坐标;若不存在,请说明理由.
如图,I是△ABC的内心,∠BAC的平分线与△ABC的外接圆相交于点D,交BC于点E.
(1)求证:BD=ID;
(2)求证:ID2=DE•DA.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.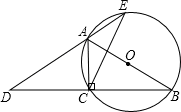
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.