已知正方形的中点为直线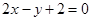 和
和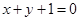 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为 ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
设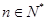 ,圆
,圆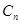 :
: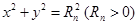 与
与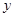 轴正半轴的交点为
轴正半轴的交点为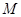 ,与曲线
,与曲线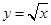 的交点为
的交点为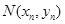 ,直线
,直线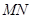 与
与 轴的交点为
轴的交点为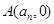 .
.
(1)用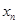 表示
表示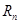 和
和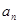 ;
;
(2)若数列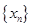 满足:
满足: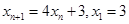 .
.
①求常数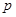 的值使数列
的值使数列 成等比数列;
成等比数列;
②比较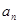 与
与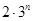 的大小.
的大小.
设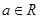 ,函数
,函数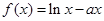 .
.
(1)讨论函数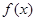 的单调区间和极值;
的单调区间和极值;
(2)已知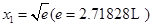 和
和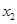 是函数
是函数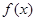 的两个不同的零点,求
的两个不同的零点,求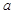 的值并证明:
的值并证明: .
.
已知圆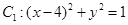 ,圆
,圆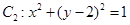 ,圆
,圆 ,
,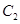 关于直线
关于直线 对称.
对称.
(1)求直线 的方程;
的方程;
(2)直线 上是否存在点
上是否存在点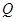 ,使
,使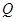 点到
点到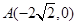 点的距离减去
点的距离减去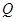 点到
点到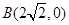 点的距离的差为
点的距离的差为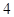 ,如果存在求出
,如果存在求出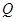 点坐标,如果不存在说明理由.
点坐标,如果不存在说明理由.
如图,三棱锥 中,
中,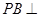 底面
底面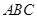 ,
,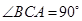 ,
, ,
,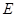 为
为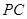 的中点,
的中点,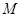 为
为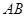 的中点,点
的中点,点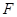 在
在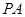 上,且
上,且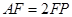 .
.
(1)求证: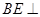 平面
平面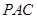 ;
;
(2)求证: 平面
平面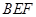 ;
;
(3)求三棱锥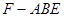 的体积.
的体积. 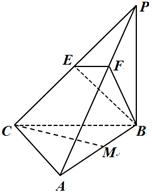
文科班某同学参加广东省学业水平测试,物理、化学、生物获得等级 和获得等级不是
和获得等级不是 的机会相等,物理、化学、生物获得等级
的机会相等,物理、化学、生物获得等级 的事件分别记为
的事件分别记为 、
、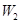 、
、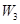 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是 的事件分别记为
的事件分别记为 、
、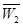 、
、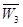 .
.
(1)试列举该同学这次水平测试中物理、化学、生物成绩是否为 的所有可能结果(如三科成绩均为
的所有可能结果(如三科成绩均为 记为
记为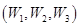 );
);
(2)求该同学参加这次水平测试获得两个 的概率;
的概率;
(3)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于 ,并说明理由.
,并说明理由.