【改编】已知圆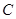 :
:
(1)平面上有两点 ,求过点
,求过点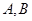 两点的直线
两点的直线 被圆
被圆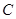 截得的弦长;
截得的弦长;
(2)已知过点 的直线
的直线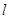 平分圆
平分圆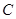 的周长,
的周长, 是直线
是直线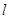 上的动点,求
上的动点,求 的最大值.
的最大值.
(3) 若 是
是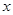 轴上的动点,
轴上的动点,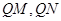 分别切圆
分别切圆 于
于 两点.
两点.
试问:直线 是否恒过定点?如是,求出定点坐标,如不是,说明理由.
是否恒过定点?如是,求出定点坐标,如不是,说明理由.
已知椭圆C: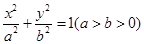 的离心率为
的离心率为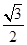 ,且C上任意一点到两个焦点的距离之和都为4.
,且C上任意一点到两个焦点的距离之和都为4.
(Ⅰ)求椭圆C的方程;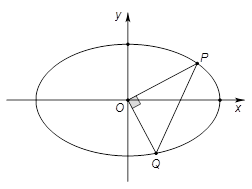
(Ⅱ)设直线 与椭圆交于P、Q,O为坐标原点,若
与椭圆交于P、Q,O为坐标原点,若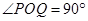 ,求证
,求证 为定值.
为定值.
有20名学生参加某次考试,成绩(单位:分)的频率分布直方图如图所示: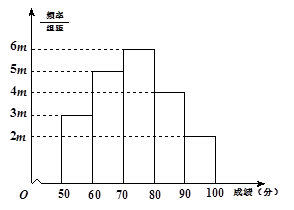
(Ⅰ)求频率分布直方图中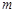 的值;
的值;
(Ⅱ)分别求出成绩落在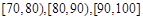 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在 的学生中任选2人,求所选学生的成绩都落在
的学生中任选2人,求所选学生的成绩都落在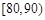 中的概率.
中的概率.
如图,在底面为平行四边形的四棱锥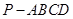 中,
中,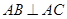 ,
, 平面
平面 ,且
,且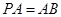 ,点
,点 是
是 的中点.
的中点.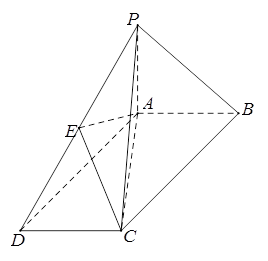
(Ⅰ)求证: 平面
平面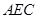 ;
;
(Ⅱ)若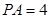 ,求点
,求点 到平面
到平面 的距离.
的距离.
在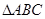 中,内角
中,内角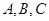 对边分别为
对边分别为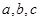 ,且
,且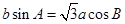 .
.
(Ⅰ)求角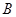 的大小;
的大小;
(Ⅱ)若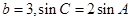 ,求
,求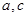 的值.
的值.
已知函数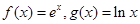 ,
,
(1)求证: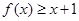 ;
;
(2)设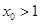 ,求证:存在唯一的
,求证:存在唯一的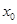 使得g(x)图象在点A(
使得g(x)图象在点A( )处的切线
)处的切线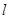 与y=f(x)图象也相切;
与y=f(x)图象也相切;
(3)求证:对任意给定的正数a,总存在正数x,使得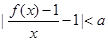 成立.
成立.