设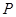 是圆
是圆 上的点,过
上的点,过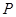 作直线
作直线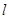 垂直
垂直 轴于点
轴于点 ,
,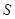 为
为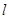 上一点,且
上一点,且 ,当点
,当点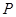 在圆上运动时,记点
在圆上运动时,记点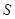 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设动点 满足
满足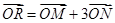 ,其中
,其中 是曲线
是曲线 上的点,
上的点,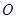 为原点,直线
为原点,直线 与
与 的斜率之积为
的斜率之积为 ,求证:
,求证: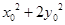 为定值.
为定值.
)如图所示,在三棱锥P-ABC中,AB=BC=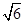 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=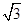 .
.
(1)证明:△PBC为直角三角形;
(2)求直线AP与平面PBC所成角的正弦值.
如图所示,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.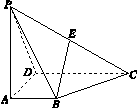
(1)求证:BE∥平面PAD;
(2)若BE⊥平面PCD,求平面EBD与平面BDC夹角的余弦值.
已知n∈N*,数列{dn}满足dn= ,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,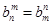 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,…,第an项删去后,剩余的项按从小到大的顺序排成新数列{cn},求数列{cn}的前2013项和T2013.
数列{an}的前n项和为Sn=2an-2,数列{bn}是首项为a1,公差不为零的等差数列,且b1,b3,b11成等比数列.
(1)求数列{an}与{bn}的通项公式;
(2)求证: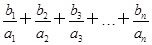 <5.
<5.
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.