(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
 人 人 |
| 社会人士 |
600人 |
 人 人 |
 人 人 |
(1)已知在全体样本中随机抽取 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为 ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
(本小题满分12分)
已知函数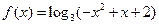 的定义域为集合
的定义域为集合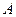 ,
,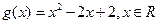 的值域为集合
的值域为集合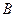 ,
,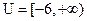 .(1)求
.(1)求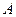 和
和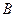 ; (2)求
; (2)求 、
、 .
.
(本小题满分14分)给定函数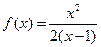
(1)试求函数 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列 满足,
满足,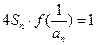 求证:
求证: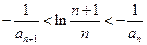 ;
;
(3)设 ,
,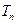 为数列
为数列 的前
的前 项和,求证:
项和,求证: 。
。
(本小题满分14分)
如图,已知曲线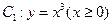 与曲线
与曲线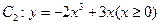 交于点
交于点 .直线
.直线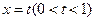 与曲线
与曲线 分别相交于点
分别相交于点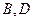 .
.
(Ⅰ)写出四边形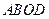 的面
的面 积
积 与
与 的函数关系
的函数关系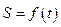 ;
;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 的最大值.
的最大值.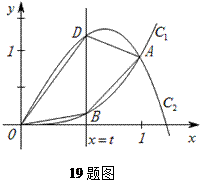
(本小题满分14分)等比数列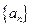 中,
中,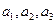 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且
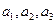 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行[来 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ) 求数列
求数列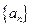 的通项公式;
的通项公式;
(Ⅱ)若数列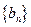 满足
满足 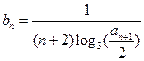 ,记数列
,记数列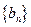 的前n项和为
的前n项和为 ,证明
,证明