(本小题满分14分)
如图,已知曲线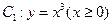 与曲线
与曲线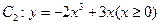 交于点
交于点 .直线
.直线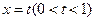 与曲线
与曲线 分别相交于点
分别相交于点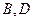 .
.
(Ⅰ)写出四边形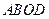 的面
的面 积
积 与
与 的函数关系
的函数关系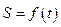 ;
;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 的最大值.
的最大值.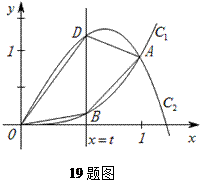
已知动圆C经过点(0,m) (m>0),且与直线y=-m相切,圆C被x轴截得弦长的最小值为1,记该圆的圆心的轨迹为E.
(Ⅰ)求曲线E的方程;
(Ⅱ)是否存在曲线C与曲线E的一个公共点,使它们在该点处有相同的切线?若存在,求出切线方程;若不存在,说明理由.
已知函数
(Ⅰ)若 在(0,
在(0, )单调递减,求a的最小值
)单调递减,求a的最小值
(Ⅱ)若 有两个极值点,求a的取值范围.
有两个极值点,求a的取值范围.
如图,直三棱柱 中,AB=BC,
中,AB=BC, ,Q是AC上的点,AB1//平面BC1Q.
,Q是AC上的点,AB1//平面BC1Q.
(Ⅰ)确定点Q在AC上的位置;
(Ⅱ)若QC1与平面BB1C1C所成角的正弦值为 ,求二面角Q-BC1—C的余弦值.
,求二面角Q-BC1—C的余弦值.
某校学习小组开展“学生语文成绩与外语成绩的关系”的课题研究,对该校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
(Ⅰ)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?
(Ⅱ)将上述调查所得到的频率视为概率,从该校高二年级学生成绩中,有放回地随机抽取3名学生的成绩,记抽取的3 个成绩中语文,外语两科成绩至少有一科优秀的个数为X ,求X的分布列和期望E(x).
 |
0.010 |
0.005 |
0.001 |
 |
6.635 |
7.879 |
10.828 |
附:
△ABC的内角A,B,C的对边分别为a,b,c,已知ac=b2-a2,A= ,求B.
,求B.