（本小题满分13分，（1）小问3分，（2）小问4分，（3）小问6分）
对于函数
,若存在实数对（
）,使得等式
对定义域中的每一个
都成立,则称函数是“（）型函数”．
（1）判断函数
是否为 “（）型函数”，并说明理由；
（2）若函数
是“（）型函数”,求出满足条件的一组实数对
；
（3）已知函数
是“（）型函数”,对应的实数对为（1,4）．当
时,
,若当
时,都有
,试求
的取值范围．
已知各项均为正数的数列{an}的前n项和为Sn,首项为a1,且
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)若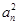
=
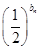,设cn=
,求数列{cn}的前n项和Tn.
在等比数列{an}中,a2a3=32,a5=32.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,求S1+2S2+…+nSn.
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=3x+1上,n∈N*.
(1)当实数t为何值时,数列{an}是等比数列?
(2)在(1)的结论下,设bn=log4an+1,cn=an+bn,Tn是数列{cn}的前n项和,求Tn.
已知数列{an}的前n项和为Sn,且有a1=2,Sn=2an-2.
(1)求数列an的通项公式;
(2)若bn=nan,求数列{bn}的前n项和Tn.
已知数列{an}满足:a1=1,a2=2,2an=an-1+an+1(n≥2,n∈N*),数列{bn}满足b1=2,anbn+1=2an+1bn.
(1)求数列{an}的通项an;
(2)求证:数列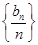
为等比数列,并求数列{bn}的通项公式.