如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.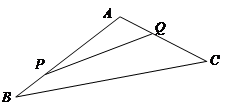
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?
设函数 .
.
(1)当 时,
时,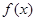 取得极值,求
取得极值,求 的值;
的值;
(2)若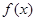 在
在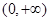
 内为增函数,求
内为增函数,求 的取值范围;
的取值范围;
(3)设 ,是否存在正实数
,是否存在正实数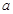 ,使得对任意
,使得对任意 ,都有
,都有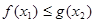 成立?
成立?
若存在,求实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. 
右图为一简单组合体,其底面 为正方形,
为正方形,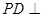 平面
平面 ,
,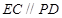 ,
,
且
(1)求证: 平面
平面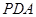 ;(2)求
;(2)求 与平面
与平面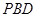 所成角的大小.
所成角的大小.
已知在等比数 列
列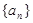 中,
中,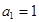 ,且
,且 是
是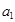 和
和 的等差中项.
的等差中项.
(1 )求数列
)求数列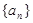 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,求
,求 的前
的前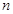 项和
项和 .
.
已知:A、B、C是 的内角,
的内角,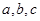 分别是其对边长,向量
分别是其对边长,向量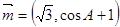 ,
, ,且
,且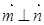 .
.
(1)求角A的大小;(2)若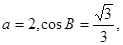 求
求 的长
的长
已知二次函数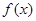 满足:①当
满足:①当 时有极值,②图象与y轴交点的纵坐标为
时有极值,②图象与y轴交点的纵坐标为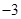 ,且在该点处的切线与直线
,且在该点处的切线与直线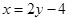 垂直
垂直
(I)求f(1)的值
(II)求函数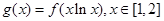 的值域
的值域
(III)若曲线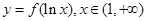 上任意一点处的切线的斜率恒大于
上任意一点处的切线的斜率恒大于 ,求
,求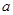 的取值范围
的取值范围