【改编】(本小题满分14分)已知函数已知函数 (
( ,
, ).
).
(1)当 时,求函数
时,求函数 在区间
在区间 上的最值;
上的最值;
(2)若 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围.
的取值范围.
(本小题满分12分)
已知向量 ="(sinA,cosA),"
="(sinA,cosA),"  =
=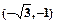 ,
,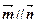 ,且A为锐角.
,且A为锐角.
(1)求角A的大小;
(2)求函数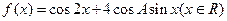 取最大值时x的集合.
取最大值时x的集合.
(本小题满分10分)
设 是两个不共线向量,已知
是两个不共线向量,已知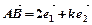 ,
, ,
, 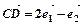 ,若三点A, B, D共线,求实数k的值。
,若三点A, B, D共线,求实数k的值。
(本小题满分12分)
如下图所示:某地一天从6~14时的温度变化曲线近似满足函数: ,求这段曲线的解析式。
,求这段曲线的解析式。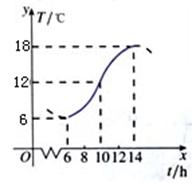
定义:若数列 满足
满足 ,则称数列
,则称数列 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列 中,
中, ,点
,点 在函数
在函数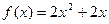 的图像上,其中
的图像上,其中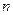 为正整数。
为正整数。
(Ⅰ)证明:数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列 为等比数列。
为等比数列。
(Ⅱ)设(Ⅰ)中“平方递推数列”的前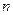 项之积为
项之积为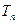 ,即
,即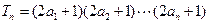 ,求数列
,求数列 的通项及
的通项及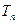 关于
关于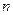 的表达式。
的表达式。
(Ⅲ)记 ,求数列
,求数列 的前
的前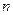 项之和
项之和 ,并求使
,并求使 的
的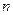 的最小值。
的最小值。
设常数 ,函数
,函数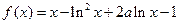
 .
.
(Ⅰ)令
 ,求
,求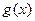 的最小值,并比较
的最小值,并比较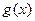 的最小值与零的大小;
的最小值与零的大小;
(Ⅱ)求证: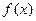 在
在 上是增函数;
上是增函数;
(Ⅲ)求证:当 时,恒有
时,恒有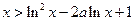 .
.