深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为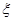 ,求
,求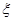 的分布列和数学期望;
的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
已知向量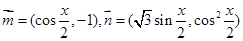 ,设函数
,设函数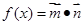 +1
+1
(1)若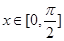 ,
, 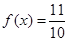 ,求
,求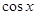 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是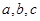 ,且满足
,且满足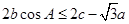 ,求
,求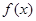 的取值范围.
的取值范围.

 已知
已知 ,
,
(1)求 解析式
解析式
(2)若函数 与
与 关于直线
关于直线 对称,若对任意实数
对称,若对任意实数
恒有 成立,求
成立,求 取值范围
取值范围
已知函数 ,
, 图象与x轴交点中,相邻两个交点之间的距离为
图象与x轴交点中,相邻两个交点之间的距离为 ,且图象最低点
,且图象最低点
(1)求 解析式
解析式
(2)将 所有点纵坐标缩短到原来的
所有点纵坐标缩短到原来的 倍(横坐标不变),在将图象向右平移
倍(横坐标不变),在将图象向右平移 个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到
个单位长度,最后在将所有点横坐标伸长到原来4倍(纵坐标不变)得到 ,求
,求 的单调递减区间
的单调递减区间
函数 函数最大值为1,最小值为
函数最大值为1,最小值为 ,求
,求