深圳市某校中学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.
(1)设第一次训练时取到的新球个数为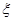 ,求
,求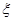 的分布列和数学期望;
的分布列和数学期望;
(2)求第二次训练时恰好取到一个新球的概率.
设数列 满足:①
满足:①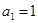 ;②所有项
;②所有项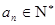 ;③
;③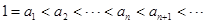 .设集合
.设集合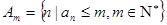 ,将集合
,将集合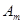 中的元素的最大值记为
中的元素的最大值记为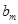 .换句话说,
.换句话说, 是数列
是数列 中满足不等式
中满足不等式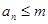 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列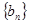 为数列
为数列 的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
的伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列 ;
;
(2)设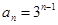 ,求数列
,求数列 的伴随数列
的伴随数列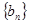 的前100之和;
的前100之和;
(3)若数列 的前
的前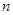 项和
项和 (其中
(其中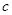 常数),试求数列
常数),试求数列 的伴随数列
的伴随数列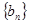 前
前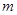 项和
项和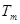 .
.
已知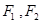 分别是椭圆
分别是椭圆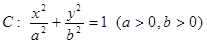 的左、右焦点,椭圆
的左、右焦点,椭圆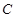 过点
过点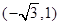 且与抛物线
且与抛物线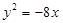 有一个公共的焦点.
有一个公共的焦点.
(1)求椭圆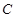 方程;
方程;
(2)斜率为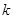 的直线
的直线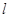 过右焦点
过右焦点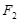 ,且与椭圆交于
,且与椭圆交于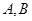 两点,求弦
两点,求弦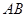 的长;
的长;
(3)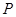 为直线
为直线 上的一点,在第(2)题的条件下,若△
上的一点,在第(2)题的条件下,若△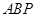 为等边三角形,求直
为等边三角形,求直
线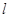 的方程.
的方程.
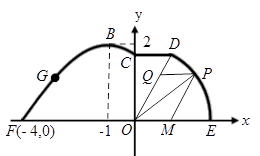
如图,在海岸线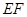 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段
一侧有一休闲游乐场,游乐场的前一部分边界为曲线段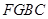 ,该曲线段是函数
,该曲线段是函数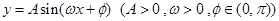 ,
,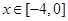 的图像,图像的最高点为
的图像,图像的最高点为 .边界的中间部分为长
.边界的中间部分为长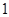 千米的直线段
千米的直线段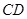 ,且
,且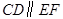 .游乐场的后一部分边界是以
.游乐场的后一部分边界是以 为圆心的一段圆弧
为圆心的一段圆弧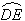 .
.
(1)求曲线段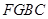 的函数表达式;
的函数表达式;
(2)曲线段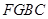 上的入口
上的入口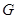 距海岸线
距海岸线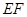 最近距离为
最近距离为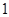 千米,现准备从入口
千米,现准备从入口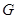 修一条笔直的景观路到
修一条笔直的景观路到 ,求景观路
,求景观路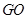 长;
长;
(3)如图,在扇形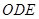 区域内建一个平行四边形休闲区
区域内建一个平行四边形休闲区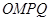 ,平行四边形的一边在海岸线
,平行四边形的一边在海岸线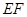 上,一边在半径
上,一边在半径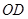 上,另外一个顶点
上,另外一个顶点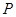 在圆弧
在圆弧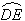 上,且
上,且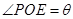 ,求平行四边形休闲区
,求平行四边形休闲区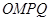 面积的最大值及此时
面积的最大值及此时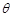 的值.
的值.
请仔细阅读以下材料:
已知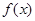 是定义在
是定义在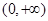 上的单调递增函数.
上的单调递增函数.
求证:命题“设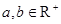 ,若
,若 ,则
,则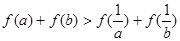 ”是真命题.
”是真命题.
证明 :因为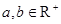 ,由
,由 得
得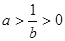 .
.
又因为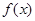 是定义在
是定义在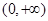 上的单调递增函数,
上的单调递增函数,
于是有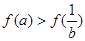 .①
.①
同理有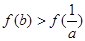 .②
.②
由①+ ②得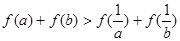 .
.
故,命题“设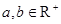 ,若
,若 ,则
,则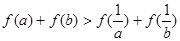 ”是真命题.
”是真命题.
请针对以上阅读材料中的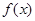 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设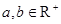 ,若
,若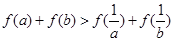 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于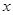 的不等式
的不等式 (其中
(其中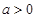 ).
).
对于集合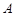 ,定义了一种运算“
,定义了一种运算“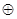 ”,使得集合
”,使得集合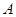 中的元素间满足条件:如果存在元素
中的元素间满足条件:如果存在元素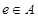 ,使得对任意
,使得对任意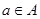 ,都有
,都有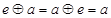 ,则称元素
,则称元素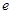 是集合
是集合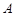 对运算“
对运算“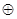 ”的单位元素.例如:
”的单位元素.例如: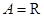 ,运算“
,运算“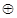 ”为普通乘法;存在
”为普通乘法;存在 ,使得对任意
,使得对任意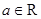 ,都有
,都有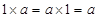 ,所以元素
,所以元素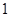 是集合
是集合 对普通乘法的单位元素.
对普通乘法的单位元素.
下面给出三个集合及相应的运算“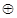 ”:
”:
①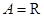 ,运算“
,运算“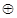 ”为普通减法;
”为普通减法;
② {
{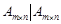 表示
表示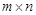 阶矩阵,
阶矩阵,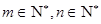 },运算“
},运算“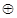 ”为矩阵加法;
”为矩阵加法;
③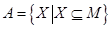 (其中
(其中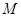 是任意非空集合),运算“
是任意非空集合),运算“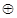 ”为求两个集合的交集.
”为求两个集合的交集.
其中对运算“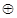 ”有单位元素的集合序号为
”有单位元素的集合序号为
| A.①② | B.①③ | C.①②③ | D.②③ |