(本小题满分13分)已知 为椭圆
为椭圆 的左,右焦点,点
的左,右焦点,点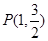 在椭圆上,且
在椭圆上,且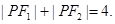
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过 的直线
的直线 分别交椭圆
分别交椭圆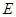 于
于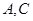 和
和 ,且
,且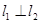 ,问是否存在常数
,问是否存在常数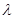 ,使得
,使得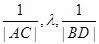 成等差数列?若存在,求出
成等差数列?若存在,求出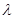 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分13分)已知函数f(x)=x2+ax+b的两个零点是-2和3
(1)求a+b的值。(2)求不等式af(-2x)>0的解集。
(本小题满分13分) 已知函数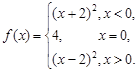
(1)写出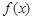 的单调区间;
的单调区间;
(2)若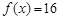 ,求相应的值。
,求相应的值。
(本小题满分13分) 已知命题p:x∈A={x|a-1<x<a+1,x∈R},命题
q:x∈B={x|x2-4x+3≥0}.
(1)或A∩B=∅,A∪B=R,求实数a
(2)若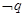 是p的必要条件,求实数a.
是p的必要条件,求实数a.
(本小题满分13分) 记函数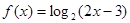 的定义域为集合M,函数
的定义域为集合M,函数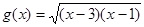 的定义域为集合N,集合C={x|m-1<x<m+1,m∈R}求:
的定义域为集合N,集合C={x|m-1<x<m+1,m∈R}求:
(1)集合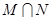 ,
,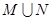 (2)若
(2)若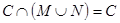 ,求实数m的取值范围
,求实数m的取值范围
已知等差数列数列 的前
的前 项和为
项和为 ,等比数列
,等比数列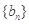 的各项均为正数,公比是
的各项均为正数,公比是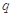 ,且满足:
,且满足: .
.
(Ⅰ)求 与
与 ;
;
(Ⅱ)设 ,若
,若 满足:
满足: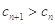 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围.
的取值范围.