在直角坐标系 中,动点
中,动点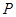 与定点
与定点 的距离和它到定直线
的距离和它到定直线 的距离之比是
的距离之比是 ,设动点
,设动点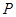 的轨迹为
的轨迹为 ,
,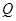 是动圆
是动圆
 上一点.
上一点.
(1)求动点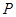 的轨迹
的轨迹 的方程;
的方程;
(2)设曲线 上的三点
上的三点 与点
与点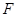 的距离成等差数列,若线段
的距离成等差数列,若线段 的垂直平分线与
的垂直平分线与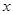 轴的交点为
轴的交点为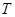 ,求直线
,求直线 的斜率
的斜率 ;
;
(3)若直线 与
与 和动圆
和动圆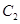 均只有一个公共点,求
均只有一个公共点,求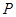 、
、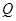 两点的距离
两点的距离 的最大值.
的最大值.
在长方体 中,
中,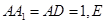 为线段
为线段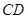 中点.
中点.
(1)求直线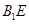 与直线
与直线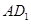 所成的角的余弦值;
所成的角的余弦值;
(2)若 ,求二面角
,求二面角 的大小;
的大小;
(3)在棱 上是否存在一点
上是否存在一点 ,使得
,使得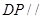 平面
平面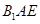 ?若存在,求
?若存在,求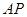 的长;若不存在,说明理由.
的长;若不存在,说明理由.
某工厂拟建一座平面图为矩形,面积为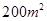 的三段式污水处理池,池高为1
的三段式污水处理池,池高为1 ,如果池的四周墙壁的建造费单价为
,如果池的四周墙壁的建造费单价为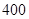 元
元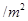 ,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为
,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为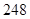 元
元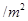 ,池底的建造费单价为
,池底的建造费单价为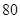 元
元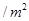 ,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
如图,四棱锥S﹣ABCD的底面为正方形,SD⊥平面ABCD,SD=AD=2,请建立空间直角坐标系解决下列问题.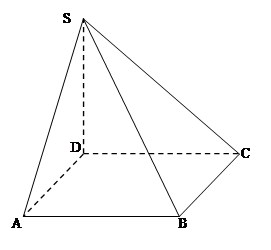
(1)求证: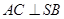 ;(2)求直线
;(2)求直线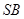 与平面
与平面 所成角的正弦值.
所成角的正弦值.
已知顶点在原点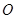 ,焦点在
,焦点在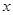 轴上的抛物线过点
轴上的抛物线过点 .
.
(1)求抛物线的标准方程;
(2)若抛物线与直线 交于
交于 、
、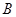 两点,求证:
两点,求证: .
.
已知命题 :任意
:任意 ,
, ,命题
,命题 :函数
:函数 在
在 上单调递减.
上单调递减.
(1)若命题 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(2)若 和
和 均为真命题,求实数
均为真命题,求实数 的取值范围.
的取值范围.