(本小题满分12分)编号分别为A1,A2, ,A16的16名校篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(1)将得分在对应区间内的人数填入相应的空格:
| 区间 |
[10,20) |
[20,30) |
[30,40] |
| 人数 |
|
|
|
(2)从得分在区间[20,30)内的运动员中随机抽取2人,①用运动员编号列出所有可能的抽取结果;②求这2人得分之和大于50的概率.
(本小题满分10分)选修4—4;坐标系与参数方程
已知直线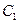 :
: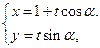 (t为参数),圆
(t为参数),圆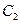 :
: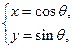 (
(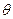 为参数),
为参数),
(Ⅰ)当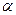 =
=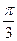 时,求
时,求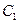 与
与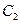 的交点坐标;
的交点坐标;
(Ⅱ)过坐标原点O作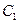 的垂线,垂足为A,P为OA的中点,当
的垂线,垂足为A,P为OA的中点,当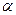 变化时,求P点轨迹的参数方程,并指出它是什么曲线;
变化时,求P点轨迹的参数方程,并指出它是什么曲线;
已知抛物线C的顶点在原点, 焦点为F(0, 1).
(Ⅰ) 求抛物线C的方程;
(Ⅱ)在抛物线C上是否存在点P, 使得过点P
的直线交C于另一点Q, 满足PF⊥QF, 且
PQ与C在点P处的切线垂直?
若存在, 求出点P的坐标; 若不存在,请说明理由.
(本题15分)已知函数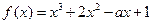 .
.
(I)若函数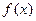 在点
在点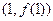 处的切线斜率为4,求实数
处的切线斜率为4,求实数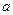 的值;
的值;
(II)若函数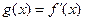 在区间
在区间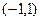 上存在零点,求实数
上存在零点,求实数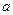 的取值。
的取值。
已知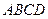 为平行四边形,
为平行四边形,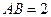 ,
,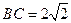 ,
, ,
,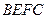 是长方形,
是长方形,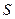 是
是 的中点,
的中点,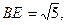 平面
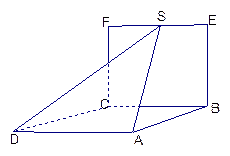
平面 平面
平面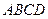 ,
,
(Ⅰ)求证: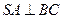 ;
;
(Ⅱ)求直线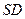 与平面
与平面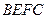 所
所
成角的正切值.
已知数列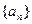 是首项为1公差为正的等差数列,数列
是首项为1公差为正的等差数列,数列 是首项为1的等比数列,设
是首项为1的等比数列,设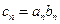
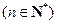 ,且数列
,且数列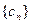 的前三项依次为1,4,12,
的前三项依次为1,4,12,
(1)求数列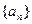 、
、 的通项公式;
的通项公式;
(2)若等差数列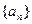 的前n项和为Sn,求数列
的前n项和为Sn,求数列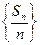 的前
的前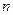 项的和Tn.
项的和Tn.