(本题15分)已知函数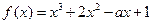 .
.
(I)若函数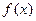 在点
在点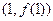 处的切线斜率为4,求实数
处的切线斜率为4,求实数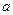 的值;
的值;
(II)若函数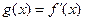 在区间
在区间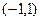 上存在零点,求实数
上存在零点,求实数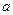 的取值。
的取值。
(本小题满分12分)如图,已知椭圆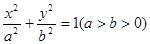 的长轴为
的长轴为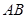 ,过点
,过点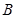 的直线
的直线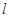 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率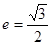
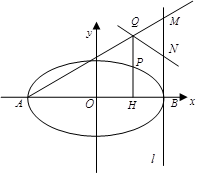
(1)求椭圆的标准方程;
(2)设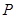 是椭圆上异于
是椭圆上异于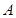 、
、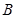 的任意一点,
的任意一点,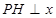 轴,
轴,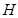 为垂足,延长
为垂足,延长 到点
到点 使得
使得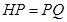 ,连接
,连接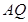 并延长交直线
并延长交直线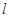 于点
于点 ,
,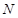 为
为 的中点.试判断直线
的中点.试判断直线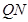 与以
与以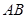 为直径的圆
为直径的圆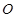 的位置关系.
的位置关系.
(本小题满分12分)已知函数f(x)=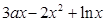 ,
, 为常数。
为常数。
(I)当 =1时,求f(x)的单调区间;
=1时,求f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求 的取值范围。
的取值范围。
(本小题满分12分)如图,在四棱锥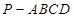 中,侧面
中,侧面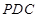 是边长为2的正三角形,且与底面垂直;底面
是边长为2的正三角形,且与底面垂直;底面 是菱形,
是菱形, ,
, 为
为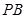 的中点.
的中点.
(1)求四棱锥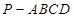 的体积;
的体积;
(2)求证: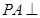 平面
平面 .
.
(本小题满分12分)已知等差数列{an}的前n项和为Sn,且a3=5,S15="225."
(1)求数列{an}的通项an;
(2)设bn= +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn.
(本小题满分12分)在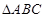 中,角
中,角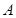 为锐角,记角
为锐角,记角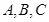 所对的边分别为
所对的边分别为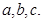 设向量
设向量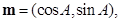
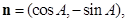 且
且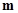 与
与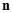 的夹角为
的夹角为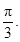
(1)求 的值及角
的值及角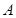 的大小;
的大小;
(2)若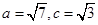 ,求
,求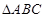 的面积
的面积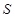 .
.