(本小题满分16分)已知数列 、
、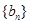 满足
满足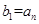 ,
,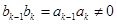 ,其中
,其中 ,则称
,则称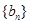 为
为 的“生成数列”.
的“生成数列”.
(1)若数列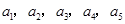 的“生成数列”是
的“生成数列”是 ,求
,求 ;
;
(2)若 为偶数,且
为偶数,且 的“生成数列”是
的“生成数列”是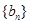 ,证明:
,证明: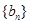 的“生成数列”是
的“生成数列”是 ;
;
(3)若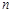 为奇数,且
为奇数,且 的“生成数列”是
的“生成数列”是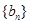 ,
,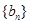 的“生成数列”是
的“生成数列”是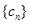 ,…,依次将数列
,…,依次将数列 ,
,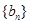 ,
,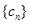 ,…的第
,…的第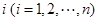 项取出,构成数列
项取出,构成数列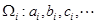 .
.
探究:数列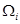 是否为等比数列,并说明理由.
是否为等比数列,并说明理由.
(本小题12分)
已知定义在R上的函 数
数 是奇函数
是奇函数
(1)求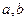 的值;
的值;
(2)判断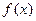 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明;
(3)若对任意的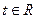 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题12分)
已知函数f (x2-3) = lg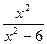 ,
,
(1) f(x)的 定义域;
定义域;
(2)判断f(x)的奇偶性;
(3)若f [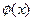 ] = lgx,求
] = lgx,求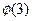 的值。
的值。
(本小题12分)
若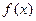 是定义在
是定义在 上的增函数,且对一切
上的增函数,且对一切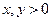 ,满足
,满足 .
.
(1)求 的值
的值
(2)若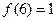 ,解不
,解不 等式
等式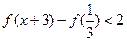 .
.
(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品。经市场预测,生产W型产品所获利润 (万元)与投入资金
(万元)与投入资金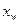 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润 (万元)与投入资金
(万元)与投入资金 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
(本小题12分)
已知奇函数 ,在
,在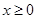 时的图象是如图所示的抛物线的一部分,
时的图象是如图所示的抛物线的一部分,
(1)请补全函数 的图象(2)求函数
的图象(2)求函数 的表达式
的表达式
(3)写出函数 的单调区间
的单调区间