在上海世博会期间,小红计划对事先选定的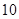 个场馆进行参观.在她选定的
个场馆进行参观.在她选定的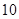 个场馆中,有
个场馆中,有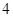 个场馆分布在
个场馆分布在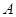 区,
区,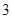 个场馆分布在
个场馆分布在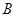 区,
区,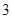 个场馆分布在
个场馆分布在 区.已知
区.已知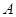 区的每个场馆的排队时间为
区的每个场馆的排队时间为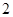 小时,
小时,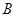 区和
区和 区的每个场馆的排队时间为
区的每个场馆的排队时间为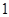 小时.参观前小红因事只能从这
小时.参观前小红因事只能从这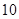 个场馆中随机选定
个场馆中随机选定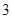 个场馆进行参观.
个场馆进行参观.
(Ⅰ)求小红每个区都参观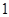 个场馆的概率;
个场馆的概率;
(Ⅱ)设小红排队时间总和为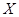 (小时),求随机变量
(小时),求随机变量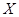 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185)得到的频率分布直方图如图所示。
(Ⅰ)求第3、4、5组的频率;
(Ⅱ)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求:第4组至少有一名学生被甲考官面试的概率?
(本小题满分12分) 若函数 的图象与直线
的图象与直线 相切,相邻切点之
相切,相邻切点之
间的距离为 。
。
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)若点 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标。
的坐标。
(13分)一个同心圆形花坛,分为两部分,中间小圆部分种植绿色灌木,周围的圆环分为n(n≥3,n∈N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的花.
⑴ 如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?
如图2,圆环分成的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵ 如图3,圆环分成的n等份为a1,a2,a3,……,an,有多少不同的种植方法?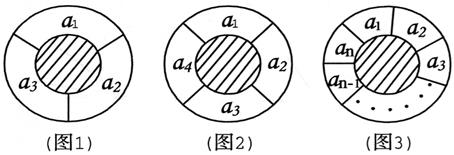
(12分) 已知数列 (n为正整数)是首项是a1,公比为q的等比数列.
(n为正整数)是首项是a1,公比为q的等比数列.
(1)求和: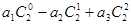 ,
,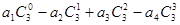
(2)由(1)的结果归纳概括出关于正整数n的一个结论,并加以证明.
(13分) 已知 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求n的值;
(2)求展开式中系数最大的项.