(本小题满分14分)设函数 ,
, 是自然对数的底数,
是自然对数的底数, ,
, 为常数.
为常数.
(1)若 在
在 处的切线
处的切线 的斜率为
的斜率为 ,求
,求 的值;
的值;
(2)在(1)的条件下,证明切线 与曲线
与曲线 在区间
在区间 至少有1个公共点;
至少有1个公共点;
(3)若 是
是 的一个单调区间,求
的一个单调区间,求 的取值范围.
的取值范围.
已知 ,
,
(1)当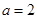 时,解不等式
时,解不等式 ;(2)若
;(2)若 ,解关于x的不等式
,解关于x的不等式 .
.
(本题12分)在平面直角坐标系 中,已知椭圆
中,已知椭圆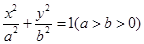 的离心率为
的离心率为 ,其焦点在圆
,其焦点在圆 上.
上.
⑴求椭圆的方程;
⑵设 、
、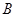 、
、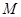 是椭圆上的三点(异于椭圆顶点),且存在锐角
是椭圆上的三点(异于椭圆顶点),且存在锐角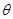 ,使
,使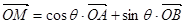 .
.
①试求直线 与
与 的斜率的乘积;
的斜率的乘积;
②试求 的值.
的值.
(本题12分)已知椭圆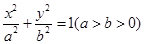 的离心率
的离心率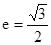 ,过
,过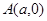 、
、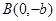 两点的直线到原点的距离是
两点的直线到原点的距离是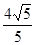 .
.
(1)求椭圆的方程 ;
(2)已知直线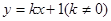 交椭圆于不同的两点
交椭圆于不同的两点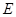 、
、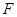 ,且
,且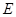 、
、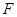 都在以
都在以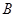 为圆心的圆上,求
为圆心的圆上,求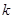 的值.
的值.
(本题12分)已知中心在原点的双曲线的右焦点为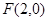 ,右顶点为
,右顶点为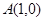 .
.
(1)试求双曲线的方程;
(2)过左焦点作倾斜角为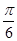 的弦
的弦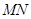 ,试求
,试求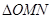 的面积(
的面积(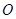 为坐标原点).
为坐标原点).
(本题12分)已知命题 :方程
:方程 表示焦点在
表示焦点在 轴上的椭圆;命题
轴上的椭圆;命题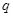 :点
:点 在圆
在圆 内.若
内.若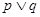 为真命题,
为真命题, 为假命题,试求实数
为假命题,试求实数 的取值范围.
的取值范围.