(本小题满分13分)
右图为一简单组合体,其底面 为正方形,
为正方形,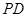
 平面
平面 ,
, //
//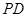 ,且
,且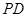 =
=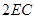 。
。
(1)求证: //平面
//平面 ;
;
(2)若 为线段
为线段 的中点,
的中点,
求证:
 平面
平面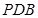 ;
;
(3)若 ,求平面
,求平面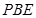 与平面
与平面
所成的二面角的大小。
已知 是无穷数列.给出两个性质:
①对于 中任意两项 ,在 中都存在一项 ,使 ;
②对于 中任意项 ,在 中都存在两项 .使得 .
(Ⅰ)若 ,判断数列 是否满足性质①,说明理由;
(Ⅱ)若 ,判断数列 是否同时满足性质①和性质②,说明理由;
(Ⅲ)若 是递增数列,且同时满足性质①和性质②,证明: 为等比数列.
已知椭圆 过点 ,且 .
(Ⅰ)求椭圆C的方程:
(Ⅱ)过点 的直线l交椭圆C于点
,直线
分别交直线
于点
.求
的值.
的直线l交椭圆C于点
,直线
分别交直线
于点
.求
的值.
已知函数 .
(Ⅰ)求曲线 的斜率等于 的切线方程;
(Ⅱ)设曲线 在点 处的切线与坐标轴围成的三角形的面积为 ,求 的最小值.
某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
|
男生 |
女生 |
|||
|
支持 |
不支持 |
支持 |
不支持 |
|
|
方案一 |
200人 |
400人 |
300人 |
100人 |
|
方案二 |
350人 |
250人 |
150人 |
250人 |
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为 ,假设该校年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为 ,试比较 与 的大小.(结论不要求证明)
在 中, ,再从条件①、条件②这两个条件中选择一个作为己知,求:
(Ⅰ)a的值:
(Ⅱ) 和 的面积.
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分.