（本小题满分14分）现有一个以OA、OB为半径的扇形池塘，在OA、OB上分别取点C、D，作DE∥OA、CF∥OB交弧AB于点E、F，且BD = AC，现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的三种的养殖区域．若OA=1km，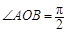
，
．
（1）求区域Ⅱ的总面积；
（2）若养殖区域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分别是15万元、20万元、10万元，记年总收入为y万元． 试问当
为多少时，年总收入最大？
过点
作一条直线和
分别相交于
两点，试求
的最大值。（其中
为坐标原点）
已知椭圆ε：
（a>b>0），动圆
：
，其中b<R<a. 若A是椭圆ε上的点，B是动圆上的点，且使直线AB与椭圆ε和动圆均相切，求A、B两点的距离
的最大值.
在周长为定值的
中，已知
，且当顶点
位于定点
时，
有最小值为
.(1)建立适当的坐标系，求顶点的轨迹方程.(2)过点
作直线与(1)中的曲线交于
、
两点，求
的最小值的集合.
在平面直角坐标系xoy中，给定三点
，点P到直线BC的距离是该点到直线AB，AC距离的等比中项。（Ⅰ）求点P的轨迹方程；（Ⅱ）若直线L经过
的内心（设为D），且与P点的轨迹恰好有3个公共点，求L的斜率k的取值范围。
已知点A
和曲线
上的点
…、
。若
、
、…、
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
,是否存在满足条件的
.若存在,求出n可取的所有值,若不存在,说明理由.