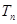(本小题满分16分)如图,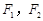 为椭圆
为椭圆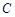 :
: (a>b>
(a>b> )的左、右焦点,
)的左、右焦点, 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率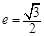 ,△
,△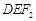 的面积为
的面积为 .若
.若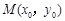 在椭圆
在椭圆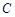 上,则点
上,则点 称为点
称为点 的一个“椭点”.直线
的一个“椭点”.直线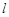 与椭圆交于
与椭圆交于 两点,
两点, 两点的“椭点”分别为
两点的“椭点”分别为 ,已知以
,已知以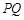 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.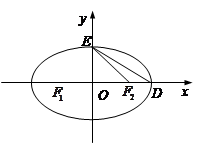
(1)求椭圆的标准方程;
(2)△ 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;
(2)求直线l被圆C截得的最短弦长.
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
| 健康指数 |
2 |
1 |
0 |
﹣1 |
| 60岁至79岁的人数 |
120 |
133[] |
34 |
13 |
| 80岁及以上的人数 |
9 |
18 |
14 |
9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,﹣1代表“生活不能自理”.
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
在△ABC中,角A,B, C所对的边分别是a,b,c,已知c=2,C= .
.
(1)若△ABC的面积等于 ,求a,b;
,求a,b;
(2)若cosA= ,求b.
,求b.
已知函数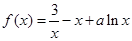 ,且
,且 是函数
是函数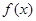 的一个极值点.
的一个极值点.
(1)求 的值;
的值;
(2)求函数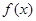 的单调区间;
的单调区间;
(3)设 ,当函数
,当函数 在区间
在区间 上零点的个数为0个,3个时,实数
上零点的个数为0个,3个时,实数 的取值范围分别为多少?(参考数据:
的取值范围分别为多少?(参考数据: ,
, )
)
若等比数列{ }的前n项和为
}的前n项和为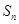 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数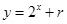 (
(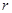 为常数)的图像上.
为常数)的图像上.
(1)求 和
和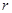 的值;
的值;
(2)记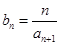 ,求数列
,求数列 的前
的前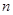 项和
项和