(本小题满分14分)设函数f(x)=(x–1)2+alnx,a∈R.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y–1=0垂直,求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若函数f(x)有两个极值点x1,x2且x1<x2,求证:f(x2)> –
– ln2.
ln2.
已知函数 .
.
(1)求 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若 在区间
在区间 上的最大值与最小值的和为
上的最大值与最小值的和为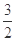 ,求
,求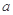 的值.
的值.
在直角坐标平面内,以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为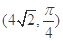 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)求直线 的直角坐标方程;
的直角坐标方程;
(2)求点 到曲线
到曲线 上的点的距离的最小值.
上的点的距离的最小值.
记函数 的定义域为集合
的定义域为集合 ,函数
,函数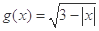 的定义域为集合
的定义域为集合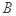 .
.
(1)求
 ;
;
(2)若 ,且
,且 ,求实数
,求实数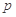 的取值范围.
的取值范围.
已知数列 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列 前
前 项和为
项和为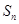 ,且满足
,且满足
(1)求数列 的通项公式;
的通项公式;
(2)求数列 前
前 项和
项和 ;
;
(3)在数列 中,是否存在连续的三项
中,是否存在连续的三项 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数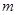 的值;若不存在,说明理由
的值;若不存在,说明理由
已知函数 (a,b均为正常数).
(a,b均为正常数).
(1)求证:函数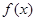 在
在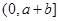 内至少有一个零点;
内至少有一个零点;
(2)设函数在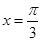 处有极值,
处有极值,
①对于一切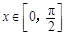 ,不等式
,不等式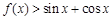 恒成立,求
恒成立,求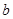 的取值范围;
的取值范围;
②若函数f(x)在区间 上是单调增函数,求实数
上是单调增函数,求实数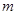 的取值范围.
的取值范围.