在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到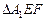 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求二面角A1-BP-E的大小。
如图,A1A是圆柱的母线,AB是圆柱底面圆的直径, C是底面圆周上异于A,B的任意一点,A1A= AB=2.
(Ⅰ)求证: BC⊥平面A1AC;
(Ⅱ)求三棱锥A1-ABC的体积的最大值.
如图,在四棱锥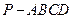 中,底面为直角梯形,
中,底面为直角梯形,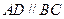 ,
,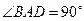 ,
,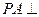 底面
底面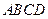 ,且
,且 ,
,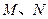 分别为
分别为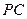 、
、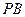 的中点。
的中点。
(Ⅰ)求证: ;
;
(Ⅱ)求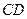 与平面
与平面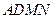 所成角的正弦值。
所成角的正弦值。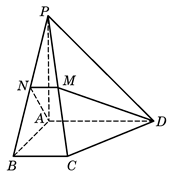
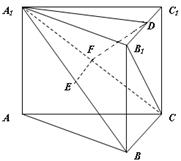
如图,在直三棱柱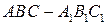 中,
中,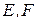 分别是
分别是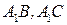 的中点,点
的中点,点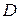 在
在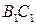 上,
上,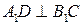
求证:(Ⅰ)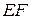 ∥平面
∥平面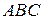
(Ⅱ)平面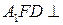 平面
平面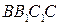
将圆心角为1200,面积为3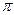 的扇形,作为圆锥的侧面,求圆锥的表面积和体积.
的扇形,作为圆锥的侧面,求圆锥的表面积和体积.