

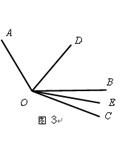
(1)如1所示,已知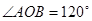 ,
, 平分
平分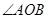 ,
,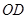 、
、 分别平分
分别平分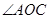 、
、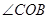 ,求
,求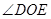 的度数;
的度数;
(2)如图2,在(1)中把“ 平分
平分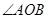 ”改为“
”改为“ 是
是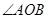 内任意一条射线”,其他任何条件都不变,试求
内任意一条射线”,其他任何条件都不变,试求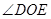 的度数;
的度数;
(3)如图3,在(1)中把“ 平分
平分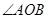 ”改为“
”改为“ 是
是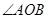 外的一条射线且点
外的一条射线且点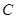 与点
与点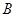 在直线
在直线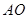 的同侧”,其他任何条件都不变,请你直接写出
的同侧”,其他任何条件都不变,请你直接写出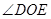 的度数.
的度数.
某跳水队为了解运动员的年龄情况,作了一次年龄调查,根据跳水运动员的年龄(单位:岁),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
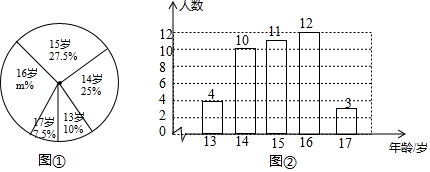
(1)本次接受调查的跳水运动员人数为 ,图①中 的值为 ;
(2)求统计的这组跳水运动员年龄数据的平均数、众数和中位数.
解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:

(4)原不等式组的解集为 .
已知抛物线 的顶点为 ,与 轴的交点为 ,点 .
(Ⅰ) 求点 , 的坐标;
(Ⅱ) 将抛物线 向上平移得到抛物线 ,点 平移后的对应点为 ,且 .
①求抛物线 的解析式;
②若点 关于直线 的对称点为 ,射线 与抛物线 相交于点 ,求点 的坐标 .
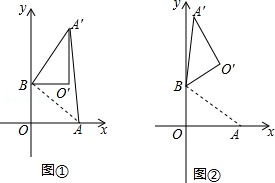
在平面直角坐标系中, 为原点,点 ,点 ,把 绕点 逆时针旋转,得△ ,点 , 旋转后的对应点为 , ,记旋转角为 .
(Ⅰ)如图①,若 ,求 的长;
(Ⅱ)如图②,若 ,求点 的坐标;
(Ⅲ)在(Ⅱ)的条件下,边 上 的一点 旋转后的对应点为 ,当 取得最小值时,求点 的坐标(直接写出结果即可)
公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台、租车费用为400元,每辆乙种货车一次最多运送机器30台、租车费用为280元
(Ⅰ)设租用甲种货车 辆 为非负整数),试填写表格.
表一:
|
租用甲种货车的数量 辆 |
3 |
7 |
|
|
租用的甲种货车最多运送机器的数量 台 |
135 |
|
|
|
租用的乙种货车最多运送机器的数量 台 |
150 |
|
|
表二:
|
租用甲种货车的数量 辆 |
3 |
7 |
|
|
租用甲种货车的费用 元 |
|
2800 |
|
|
租用乙种货车的费用 元 |
|
280 |
|
(Ⅱ)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.