如图，在平面直角坐标系中，直线y=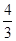
x+4分别交x轴，y轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形．
（1）直接写出点A，B的坐标，并求直线AB与CD交点E的坐标；
（2）动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发，沿线段AO以每秒1个单位长度的速度向终点O运动，过点P作PH⊥OA，垂足为H，连接NP．设点P的运动时间为t秒．
① 若△NPH的面积为1，求t的值；
② 点Q是点B关于点A的对称点，问BP+PH+HQ是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由．
如图，矩形ABCD是供一辆机动车停放的车位示意图，已知BC=2m，CD=5.4m，∠DCF=30°，请你计算车位所占的宽度EF约为多少米？（
，结果保留两位有效数字．）
先化简，再求值：
，其中a=
．
如图所示，已知抛物线的顶点为坐标原点O，矩形ABCD的顶点A，D在抛物线上，且AD平行x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为（2，1），点P（a，b）在抛物线上运动．（点P异于点O）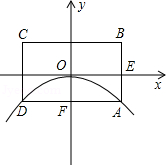
（1）求此抛物线的解析式．
（2）过点P作CB所在直线的垂线，垂足为点R，
①求证：PF=PR；
②是否存在点P，使得△PFR为等边三角形？若存在，求出点P的坐标；若不存在，请说明理由；
③延长PF交抛物线于另一点Q，过Q作BC所在直线的垂线，垂足为S，试判断△RSF的形状．
如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜
）秒．解答如下问题：
（1）当t为何值时，PQ∥BO？
（2）设△AQP的面积为S，
①求S与t之间的函数关系式，并求出S的最大值；
②若我们规定：点P、Q的坐标分别为（x1，y1），（x2，y2），则新坐标（x2﹣x1，y2﹣y1）称为“向量PQ”的坐标．当S取最大值时，求“向量PQ”的坐标．
如图，AB是⊙O的直径，动弦CD垂直AB于点E，过点B作直线BF∥CD交AD的延长线于点F，若AB=10cm．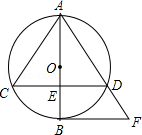
（1）求证：BF是⊙O的切线．
（2）若AD=8cm，求BE的长．
（3）若四边形CBFD为平行四边形，则四边形ACBD为何种四边形？并说明理由．