(本小题满分14分)对于定义域为 的函数
的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在
在 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间 ,使
,使 在
在 上的值域为
上的值域为 ;那么把
;那么把 (
( )叫闭函数,且条件②中的区间
)叫闭函数,且条件②中的区间 为
为 的一个“好区间”.
的一个“好区间”.
(1)求闭函数 的“好区间”;
的“好区间”;
(2)若 为闭函数
为闭函数 的“好区间”,求
的“好区间”,求 、
、 的值;
的值;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围.
的取值范围.
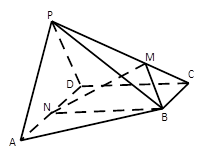
如图,四棱锥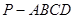 的侧面
的侧面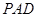 垂直于底面
垂直于底面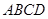 ,
,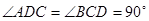 ,
,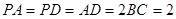 ,
,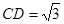 ,
, 在棱
在棱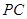 上,
上, 是
是 的中点,二面角
的中点,二面角 为
为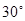
(1)求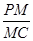 的值;
的值;
(2)求直线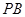 与平面
与平面 所成角的正弦值.
所成角的正弦值.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组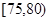 ,第2组
,第2组 ,第3组
,第3组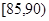 ,第4组
,第4组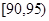 ,第5组
,第5组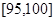 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
(1)分别求第3,4,5组的频率;
(2)若该校决定在第3,4,5 组中用分层抽样的方法抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第3组,求学生甲和学生乙同时进入第二轮面试的概率;
②学校决定在这6名学生中随机抽取2名学生接受考官 的面试,第4组中有
的面试,第4组中有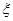 名学生被考官
名学生被考官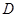 面试,求
面试,求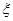 的分布列和数学期望.
的分布列和数学期望.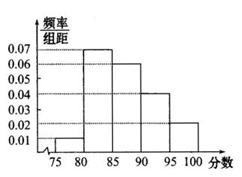
已知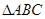 的内角
的内角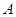 、
、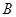 、
、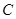 的对边分别为
的对边分别为 、
、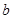 、
、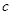 ,
,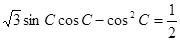 ,且
,且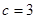
(1)求角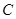 ;
;
(2)若向量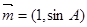 与
与 共线,求
共线,求 、
、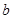 的值.
的值.
已知函数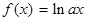 (
(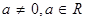 ),
),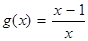 .
.
(Ⅰ)当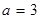 时,解关于
时,解关于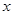 的不等式:
的不等式: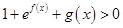 ;
;
(Ⅱ)当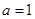 时,记
时,记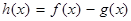 ,过点
,过点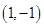 是否存在函数
是否存在函数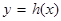 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若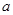 是使
是使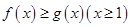 恒成立的最小值,对任意
恒成立的最小值,对任意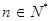 ,
,
试比较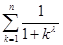 与
与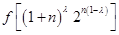 的大小(常数
的大小(常数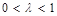 ).
).
设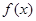 是定义在
是定义在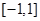 上的奇函数,函数
上的奇函数,函数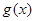 与
与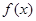 的图象关于
的图象关于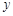 轴对称,且当
轴对称,且当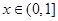 时,
时,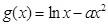 .
.
(I)求函数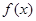 的解析式;
的解析式;
(II)若对于区间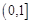 上任意的
上任意的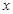 ,都有
,都有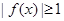 成立,求实数
成立,求实数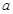 的取值范围.
的取值范围.