(本小题满分13分)已知二次函数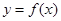 的图象的顶点坐标为
的图象的顶点坐标为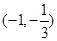 ,且过坐标原点
,且过坐标原点 .数列
.数列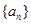 的前
的前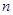 项和为
项和为 ,点
,点 在二次函数
在二次函数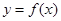 的图象上.
的图象上.
(Ⅰ)求数列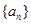 的通项公式;
的通项公式;
(Ⅱ)设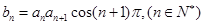 ,数列
,数列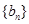 的前
的前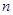 项和为
项和为 ,若
,若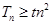 对
对 恒成立,求实数
恒成立,求实数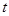 的取值范围;
的取值范围;
(Ⅲ)在数列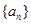 中是否存在这样一些项:
中是否存在这样一些项: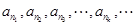

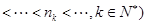 ,这些项都能够构成以
,这些项都能够构成以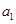 为首项,
为首项, 为公比的等比数列
为公比的等比数列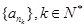 ?若存在,写出
?若存在,写出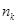 关于
关于 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
(本小题满分12分)已知黄河游览区有两艘游船,两艘游船每天上午11点出发,下午3点至5点之间返回码头,假如码头只有一个泊位,每艘游船需要停靠码头15分钟游客下完后即驶离码头,每艘油船返回时在下午3点至5点之间的任何一时刻停靠码头是等可能的,求你乘坐一艘游船游览黄河游览区,下午返回码头时,停船的泊位是空的概率。
(本小题满分12分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四张卡片,现从甲、乙两个盒子中各取出1张卡片,每张卡片被取出的可能性相等;
(Ⅰ)求取出的两张卡片标号之积能被3整除的概率;
(Ⅱ)如果小王、小李取出的两张卡片的标号相加,谁的两张卡片标号之和大则谁胜出,若小王先抽,抽出卡片的标号分别为3和4,且小王抽出的两张卡片不再放回盒中,小李再抽;求小王胜出的概率。
(本小题满分12分)以下是搜集到的开封市祥符区新房屋的销售价格 (万元)和房屋的面积
(万元)和房屋的面积 (
( )的数据: 已知变量
)的数据: 已知变量 和
和 线性相关。
线性相关。
 |
80 |
95 |
100 |
110 |
115 |
 |
18.4 |
21.6 |
23.2 |
24.8 |
27 |
(Ⅰ)求 、
、 ,及线性回归方程;
,及线性回归方程;
(Ⅱ)据(Ⅰ)的结果估计当房屋面积为 时的销售价格。
时的销售价格。
(本小题满分12分)如下图所示,从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图,观察图形,回答下列问题:
(Ⅰ) 这一组的频率和频数分别为多少?
这一组的频率和频数分别为多少?
(Ⅱ)估计这次环保知识竞赛的平均成绩。
(本小题满分12分)下图是为了计算 的值而设计的程序框图,
的值而设计的程序框图,
(Ⅰ)将(1)、(2)两处缺失的语句补上。
(Ⅱ)指出程序框图中用的是那一种类型的循环结构,并用另一种循环结构画出程序框图。