(本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和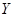 ,试求
,试求 和
和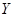 的分布列和数学期望.
的分布列和数学期望.
如图所示,四边形ABCD和四边形AB′C′D分别是矩形和平行四边形,其中各点的坐标分别为A(-1,2)、B(3,2)、C(3,-2)、D(-1,-2)、B′(3,7)、C′(3,3).求将四边形ABCD变成四边形AB′C′D的变换矩阵M.
在线性变换 =
=
 下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标.
下,直线x+y=k(k为常数)上的所有点都变为一个点,求此点坐标.
已知直线l:ax+y=1在矩阵A=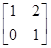 对应的变换作用下变为直线l′:x+by=1.
对应的变换作用下变为直线l′:x+by=1.
(1)求实数a、b的值;
(2)若点P(x0,y0)在直线l上,且A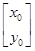 =
=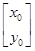 ,求点P的坐标.
,求点P的坐标.
已知矩阵M=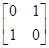 ,N=
,N= ,在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程.
,在平面直角坐标系中,设直线2x-y+1=0在矩阵MN对应的变换作用下得到的曲线F,求曲线F的方程.
在直角坐标系中,△OAB的顶点坐标O(0,0)、A(2,0),B(1,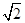 ),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=
),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M= ,N=
,N=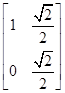 .
.