(本小题满分12分)定义在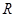 上的函数
上的函数 满足
满足 ,
, .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间;
的单调区间;
(3)如果 ,
, ,
, 满足
满足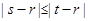 ,那么称
,那么称 比
比 更靠近
更靠近 .当
.当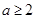 且
且 时,试比较
时,试比较 和
和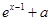 哪个更靠近
哪个更靠近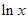 ,并说明理由.
,并说明理由.
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:82,86,87,88,91,94.把这6名学生的得分看成一个总体.
(1)求该总体的平均数与方差;
(2)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过 的概率.
的概率.
已知函数 。
。
(1)作出函数 的图象;
的图象;
(2)求出函数 的单调区间及最小值。
的单调区间及最小值。
已知函数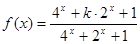 。
。
(1)若对于任意的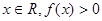 恒成立,求实数
恒成立,求实数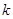 的取值范围;
的取值范围;
(2)若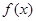 的最小值为
的最小值为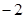 ,求实数
,求实数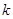 的值;
的值;
(3)若对任意的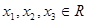 ,均存在以
,均存在以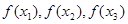 为三边长的三角形,求实数
为三边长的三角形,求实数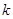 的取值范围。
的取值范围。
已知 。
。
(1)求函数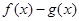 的定义域;
的定义域;
(2)判断函数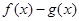 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)当a>1时,求使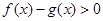 的
的 的取值范围。
的取值范围。
某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?