(本小题满分12分)已知椭圆 :
: 的上顶点为
的上顶点为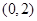 ,且离心率为
,且离心率为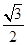 .
.
(1)求椭圆 的方程;
的方程;
(2)证明:过圆 上一点
上一点 的切线方程为
的切线方程为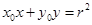 ;
;
(3)从椭圆 上一点
上一点 向圆
向圆 引两条切线,切点为
引两条切线,切点为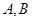 ,当直线
,当直线 分别与
分别与 轴、
轴、 轴交于
轴交于 两点时,求
两点时,求 的最小值.
的最小值.
(本小题10分)
(1)已知直线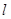 过点
过点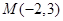 且与直线
且与直线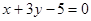 垂直,求直线
垂直,求直线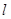 的方程.
的方程.
(2)已知直线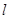 经过直线
经过直线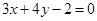 与直线
与直线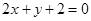 的交点
的交点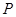 ,且平行于直线
,且平行于直线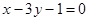 .求直线
.求直线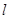 与两坐标轴围成的三角形的面积;
与两坐标轴围成的三角形的面积;
设 ,且
,且 .
.
(1) ;
;
(2) 与
与 不可能同时成立.
不可能同时成立.
已知直线 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
将曲线C的极坐标方程化为直角坐标方程;
设点 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线C 的交点为
与曲线C 的交点为 ,
, ,求
,求 的值.
的值.
【2015高考湖南,理16】(1)如图,在圆 中,相交于点
中,相交于点 的两弦
的两弦 ,
, 的中点分别是
的中点分别是 ,
, ,直线
,直线 与直线
与直线 相交于点
相交于点 ,证明:
,证明:
(1) ;
;
(2)
【2015高考新课标1,理24】选修4—5:不等式选讲
已知函数 =|x+1|-2|x-a|,a>0.
=|x+1|-2|x-a|,a>0.
(Ⅰ)当a=1时,求不等式f(x)>1的解集;
(Ⅱ)若f(x)的图像与x轴围成的三角形面积大于6,求a的取值范围.