如图1是边长为4的等边三角形,将其剪拼成一个正三棱柱模型(如图2),使它的全面积与原三角形的面积相等。D为AC上一点,且BD DC1.
DC1.

(1)求证:直线AB1∥平面BDC1
(2)求点A到平面BDC1的距离.
(本题小满12分)已知圆锥曲线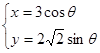 (
(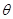 是参数)和定点
是参数)和定点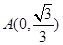 ,
,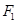 ,
,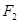 是圆锥曲线的左、右焦点.
是圆锥曲线的左、右焦点.
(1)求经过点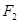 且垂直于直线
且垂直于直线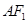 的直线
的直线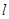 的参数方程.
的参数方程.
(2)以坐标原点为极点,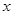 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线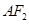 的极坐标方程.
的极坐标方程.
(本题小满分12分)已知函数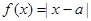 .
.
(1)若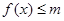 的解集为
的解集为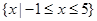 ,求实数
,求实数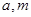 的值.
的值.
(2)当 且
且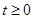 时,解关于
时,解关于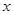 的不等式
的不等式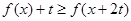 .
.
(本题小满分10分)设命题 :函数
:函数 在
在 上单调递增;
上单调递增;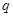 :关于
:关于 的方程
的方程 的解集只有一个子集.若“
的解集只有一个子集.若“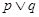 ”为真,“
”为真,“ ”为假,求实数
”为假,求实数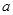 的取值范围.
的取值范围.
设函数,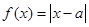
(1)当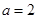 ,解不等式,
,解不等式,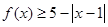 ;
;
(2)若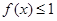 的解集为
的解集为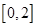 ,
, ,求证:
,求证: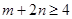
己知圆 的参数方程为
的参数方程为 (
(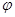 为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆
为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为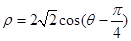 .
.
(1)将圆 的参数方程他为普通方程,将圆
的参数方程他为普通方程,将圆 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆 ,
, 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.